The Measure Of An Acute Angle 90
News Leon
Mar 31, 2025 · 6 min read
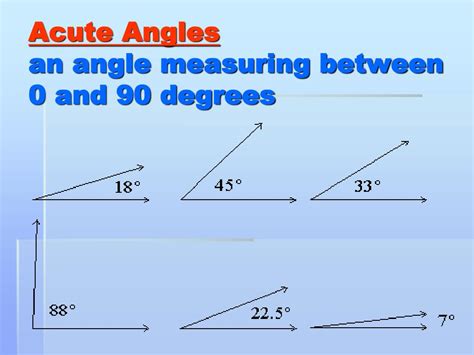
Table of Contents
The Measure of an Acute Angle: Exploring the World of Angles Less Than 90 Degrees
The world of geometry is filled with fascinating shapes and relationships, and a fundamental building block of this world is the angle. Angles, formed by two rays sharing a common endpoint (the vertex), are measured in degrees, and understanding their properties is crucial to comprehending more complex geometric concepts. This article delves into the specific measure of an acute angle, exploring its definition, properties, and applications within various mathematical fields. We will also examine how acute angles interact with other types of angles, such as right, obtuse, and reflex angles, to create a comprehensive understanding of angular measurement.
Defining Acute Angles: Less Than 90 Degrees
An acute angle is defined as an angle whose measure is less than 90 degrees but greater than 0 degrees. This simple definition lays the groundwork for understanding its unique characteristics and how it differs from other types of angles. It's important to note that the angle's measure must be strictly less than 90 degrees; an angle measuring exactly 90 degrees is a right angle, not an acute angle.
Key Characteristics:
- Measure: The defining characteristic of an acute angle is its measure, always falling within the range of 0° < x < 90°, where 'x' represents the angle's measure in degrees.
- Appearance: Visually, an acute angle appears smaller than a right angle. Imagine a corner of a square (a right angle) and then visualize a slightly smaller angle; this would represent an acute angle.
- Examples: Many everyday objects exhibit acute angles. Consider the angle formed by the hands of a clock at 2:00, the angle between two adjacent sides of a regular pentagon, or the angle at the tip of a pointed pencil.
Acute Angles in Triangles: A Cornerstone of Geometry
Triangles, fundamental shapes in geometry, are categorized based on their angles. Acute angles play a significant role in defining acute triangles. An acute triangle is a triangle in which all three angles are acute angles – meaning each angle measures less than 90 degrees. This characteristic differentiates it from other types of triangles, such as right triangles (containing one 90-degree angle) and obtuse triangles (containing one angle greater than 90 degrees).
Relationship with Other Angles: A Comparative Analysis
Understanding acute angles requires examining their relationship to other types of angles. By contrasting and comparing, we can develop a more robust understanding of angular measurement.
1. Right Angles (90 Degrees): Right angles are the benchmark against which acute angles are defined. An acute angle is always smaller than a right angle. The relationship is fundamental; acute angles and right angles are used to classify triangles.
2. Obtuse Angles (Greater Than 90 Degrees): Obtuse angles are the opposite of acute angles. They measure greater than 90 degrees but less than 180 degrees. In a triangle, the presence of an obtuse angle excludes the possibility of the triangle being an acute triangle.
3. Reflex Angles (Greater Than 180 Degrees): Reflex angles are larger than both acute and obtuse angles, measuring greater than 180 degrees but less than 360 degrees. They represent a significant rotation beyond a straight line. Reflex angles are rarely encountered in the context of triangles but are essential in other areas of geometry and trigonometry.
4. Straight Angles (180 Degrees): A straight angle is a flat line, representing a 180-degree angle. Acute angles are significantly smaller than a straight angle.
Acute Angles and Trigonometry: Fundamental Building Blocks
Trigonometry, the study of triangles and their relationships, relies heavily on the concept of acute angles. Trigonometric functions – sine, cosine, and tangent – are defined based on the ratios of sides in right-angled triangles, and these ratios are specifically defined for the acute angles within the right triangle.
For instance, in a right-angled triangle:
- Sine (sin) of an acute angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos) of an acute angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan) of an acute angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These trigonometric functions are crucial for solving problems involving triangles, particularly in fields like surveying, navigation, and engineering. The understanding of acute angles is indispensable in applying these functions accurately.
Applications of Acute Angles: Beyond the Classroom
Acute angles are not confined to theoretical geometric concepts; they have numerous practical applications in various fields:
1. Architecture and Construction: Architects and engineers extensively utilize acute angles in designing buildings, bridges, and other structures. The angles of roof pitches, structural supports, and aesthetic elements often involve acute angles.
2. Art and Design: Acute angles play a significant role in creating visual appeal and perspective in art and design. The angles of lines and shapes can drastically alter the perceived composition and dynamism of a piece.
3. Computer Graphics and Game Development: Acute angles are crucial in generating realistic 3D models and animations. The precise angles between surfaces and objects are essential for accurate rendering and simulations.
4. Navigation and Surveying: Acute angles are used extensively in surveying and navigation to determine distances, bearings, and locations. Precise angle measurements are critical for accurate mapping and route planning.
Solving Problems Involving Acute Angles: Practical Exercises
Let's explore some practical exercises to solidify our understanding of acute angles:
Example 1: Find the measure of the third angle in a triangle where two angles are 45° and 30°.
- Solution: The sum of angles in a triangle is always 180°. Therefore, the third angle is 180° - 45° - 30° = 105°. This indicates the triangle is an obtuse triangle, not an acute triangle.
Example 2: A right-angled triangle has one acute angle measuring 35°. What is the measure of the other acute angle?
- Solution: Since the sum of angles in a triangle is 180°, and one angle is 90° (the right angle), the sum of the two acute angles is 180° - 90° = 90°. Therefore, the other acute angle measures 90° - 35° = 55°.
Example 3: A regular hexagon has interior angles of 120 degrees. Explain whether you can form an acute triangle with these angles.
- Solution: No. You cannot form an acute triangle using interior angles from a regular hexagon. An acute triangle requires all angles to be less than 90 degrees. The 120-degree interior angle of the hexagon exceeds this requirement.
Further Exploration: Advanced Concepts
For those seeking a deeper understanding, further exploration into related concepts is recommended:
- Inscribed and Circumscribed Angles: These concepts explore the relationship between angles formed by chords and tangents within circles.
- Angular Measurement Systems: Delve into other units of angular measurement like radians and grads.
- Solid Geometry: Explore the concepts of dihedral angles and polyhedral angles in three-dimensional space.
Conclusion: Mastering the Acute Angle
The measure of an acute angle, less than 90 degrees, is a fundamental concept in geometry with far-reaching applications. Understanding its definition, properties, and relationship to other types of angles is crucial for comprehending more complex geometric concepts and their applications in various fields. By mastering the concept of acute angles, you open the door to a deeper understanding of the mathematical world and its practical implications. From architecture to computer graphics, the impact of acute angles is pervasive and significant, underscoring their importance in both theoretical and practical contexts. Through continued study and exploration, you can unlock a deeper appreciation for the elegance and utility of this fundamental geometric element.
Latest Posts
Latest Posts
-
Clown Fish Living Among The Tentacles Of Sea Anemone
Apr 02, 2025
-
All Squares Are Rectangles But Not All Rectangles Are Squares
Apr 02, 2025
-
A Process By Which Information Is Exchanged Between Individuals
Apr 02, 2025
-
Select The Four Statements About Plasmodium That Are True
Apr 02, 2025
-
Greatest Common Factor Of 36 And 20
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about The Measure Of An Acute Angle 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
