All Squares Are Rectangles But Not All Rectangles Are Squares
News Leon
Apr 02, 2025 · 5 min read
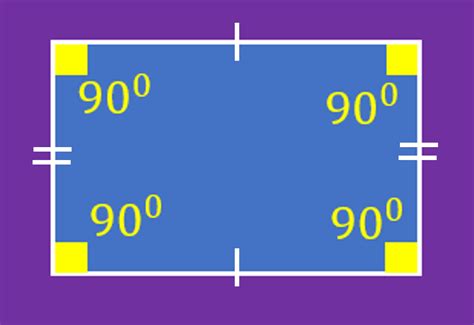
Table of Contents
All Squares Are Rectangles, But Not All Rectangles Are Squares: A Deep Dive into Quadrilaterals
The seemingly simple statement, "All squares are rectangles, but not all rectangles are squares," encapsulates a fundamental concept in geometry that often trips up beginners. Understanding this distinction requires a deep dive into the properties of quadrilaterals, specifically rectangles and squares. This article will explore these shapes, their defining characteristics, and the logical reasoning behind the core statement. We'll also touch upon the broader implications of this concept in mathematics and beyond.
Defining Quadrilaterals: The Foundation
Before we delve into rectangles and squares, let's establish a clear understanding of quadrilaterals. A quadrilateral is any polygon (a closed, two-dimensional shape) with four sides. Many different types of quadrilaterals exist, each with its unique set of properties. Some common examples include:
- Trapezoids: Quadrilaterals with at least one pair of parallel sides.
- Parallelograms: Quadrilaterals with two pairs of parallel sides.
- Rectangles: Parallelograms with four right angles.
- Squares: Rectangles with four equal sides.
- Rhombuses: Parallelograms with four equal sides.
Understanding Rectangles: The Defining Characteristics
A rectangle is a quadrilateral characterized by the following properties:
- Four sides: Like all quadrilaterals, a rectangle has four sides.
- Four right angles: This is the crucial defining property of a rectangle. Each interior angle measures exactly 90 degrees.
- Opposite sides are parallel and equal in length: This property stems from the fact that a rectangle is a parallelogram.
These properties lead to several important consequences:
- Diagonals bisect each other: The diagonals of a rectangle (lines connecting opposite corners) intersect at their midpoints.
- Opposite sides are congruent: The lengths of opposite sides are equal.
Exploring Squares: Rectangles with Added Constraints
A square is a special type of rectangle that adds an extra constraint:
- All sides are equal in length: This is the key difference between a square and a rectangle. A square possesses all the properties of a rectangle but with the additional requirement of equal side lengths.
This added constraint leads to further properties:
- Diagonals are perpendicular bisectors: The diagonals of a square not only bisect each other but also intersect at right angles.
- Diagonals are equal in length: Unlike some parallelograms, the diagonals of a square have equal lengths.
The Logical Relationship: Why All Squares Are Rectangles
The statement "all squares are rectangles" is a true statement because a square satisfies all the requirements of a rectangle. Consider the definition of a rectangle: a quadrilateral with four right angles and opposite sides parallel and equal. A square inherently fulfills all these conditions. Since a square is a type of rectangle, it inherits all the properties of a rectangle. This is a clear example of a subset relationship in set theory: the set of squares is a subset of the set of rectangles.
The Converse: Why Not All Rectangles Are Squares
The statement "not all rectangles are squares" is also true. While a square is a specific type of rectangle, many rectangles do not have equal sides. A rectangle can have sides of different lengths while still maintaining its four right angles and parallel opposite sides. The defining properties of a rectangle do not necessitate equal side lengths. The set of rectangles is significantly larger than the set of squares; it encompasses all squares plus a vast number of other shapes with unequal sides but four right angles.
Visualizing the Relationship: Venn Diagrams
A Venn diagram is a useful visual tool to illustrate the relationship between squares and rectangles. Imagine two overlapping circles. The smaller circle represents "squares," and the larger circle represents "rectangles." The smaller circle is entirely contained within the larger circle, demonstrating that all squares are rectangles. However, there's a significant portion of the larger circle that lies outside the smaller circle, representing the rectangles that are not squares.
Real-World Applications: Beyond Theoretical Geometry
The distinction between squares and rectangles has practical applications in various fields:
- Construction and Engineering: Understanding the properties of squares and rectangles is crucial in designing buildings, bridges, and other structures. Squares provide stability and symmetry, while rectangles offer flexibility in design.
- Art and Design: Artists and designers utilize squares and rectangles to create aesthetically pleasing compositions. The proportions and relationships between these shapes influence the overall feel and balance of a design.
- Computer Graphics and Programming: Squares and rectangles are fundamental shapes in computer graphics and programming. They are used to create user interfaces, games, and animations.
- Manufacturing and Packaging: Many products are packaged in rectangular or square containers. Understanding the dimensions and area of these shapes is important for optimizing packaging efficiency.
Extending the Concept: Hierarchy of Quadrilaterals
The relationship between squares and rectangles demonstrates a broader hierarchical structure within the family of quadrilaterals. We can visualize this hierarchy as a tree diagram:
- Quadrilaterals
- Trapezoids
- Parallelograms
- Rectangles
- Squares
- Rhombuses
- Squares
- Rectangles
This hierarchy shows that squares are a subset of rectangles, which are a subset of parallelograms, which in turn are a subset of quadrilaterals. Each level adds specific constraints and properties to the shapes, creating a rich and interconnected system of geometric figures.
Beyond Geometry: Logical Reasoning and Set Theory
The discussion of squares and rectangles provides a valuable exercise in logical reasoning and set theory. The statement "all squares are rectangles, but not all rectangles are squares" illustrates fundamental concepts like:
- Necessary and sufficient conditions: Having four right angles and opposite sides parallel and equal is a necessary but not sufficient condition for a shape to be a square. Equal side lengths are a necessary and sufficient condition for a rectangle to be a square.
- Conditional statements: Statements like "If a shape is a square, then it is a rectangle" are conditional statements that follow the general form "If P, then Q."
- Converse statements: The converse of "If P, then Q" is "If Q, then P." The converse of a true statement is not always true, as exemplified by the relationship between squares and rectangles.
Conclusion: A Foundation for Further Exploration
The simple statement "all squares are rectangles, but not all rectangles are squares" serves as a gateway to deeper understanding in geometry, logic, and set theory. By exploring the defining characteristics of these shapes, we gain valuable insights into the relationships between different geometric figures and the power of precise mathematical definitions. This fundamental concept is not just a theoretical exercise; it has practical applications across various fields. Mastering this concept provides a solid foundation for more advanced mathematical explorations. The beauty lies in the elegance of its simplicity and its broad implications in understanding the world around us.
Latest Posts
Latest Posts
-
Why Are Fleas Hard To Squish
Apr 03, 2025
-
How Many Chromosomes In A Daughter Cell
Apr 03, 2025
-
Why Do Bones Heal Quicker Than Cartilage
Apr 03, 2025
-
Can Magnitude Be Negative In Physics
Apr 03, 2025
-
What Is The Area Of Triangle Rst
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about All Squares Are Rectangles But Not All Rectangles Are Squares . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
