The Amount Of Space An Object Occupies
News Leon
Mar 31, 2025 · 5 min read
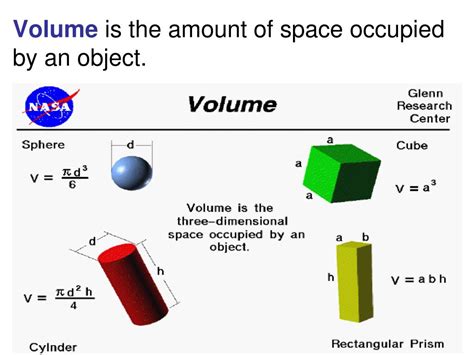
Table of Contents
The Amount of Space an Object Occupies: A Deep Dive into Volume
The amount of space an object occupies is a fundamental concept in physics and mathematics, formally known as volume. Understanding volume is crucial in various fields, from everyday life to complex scientific research. This comprehensive guide delves into the intricacies of volume, exploring its definition, measurement, calculation for different shapes, and applications across various disciplines.
Defining Volume: More Than Just Space
Volume isn't simply the space an object takes up; it's the three-dimensional extent of that space. It quantifies the amount of space enclosed within a three-dimensional boundary. Imagine filling a container with water: the amount of water needed to completely fill the container represents its volume. This concept extends beyond tangible objects; we can also talk about the volume of gases, liquids, and even abstract shapes.
The Importance of Units: Measuring Volume
Measuring volume necessitates the use of appropriate units. The most common unit is the cubic meter (m³) in the International System of Units (SI). Other common units include:
- Cubic centimeter (cm³): Frequently used for smaller objects.
- Liter (L): A metric unit of volume equal to 1000 cm³.
- Gallon (gal): A unit primarily used in the United States and the United Kingdom.
- Cubic foot (ft³): Commonly used in the United States and the United Kingdom.
Understanding the relationships between these units is essential for accurate calculations and conversions. For instance, 1 m³ is equivalent to 1,000,000 cm³ or 1000 L.
Calculating Volume: A Shape-Specific Approach
Calculating the volume of an object depends heavily on its shape. Different geometrical shapes require different formulas. Let's explore some common shapes and their corresponding volume formulas:
1. Cubes and Rectangular Prisms
These are the simplest shapes to calculate volume for. The formula is straightforward:
Volume = length × width × height
For a cube, where all sides are equal (length = width = height = s), the formula simplifies to:
Volume = s³
2. Cylinders
Cylinders, with their circular base and uniform height, have a slightly more complex formula:
Volume = π × radius² × height
Where 'π' (pi) is approximately 3.14159, 'radius' is the radius of the circular base, and 'height' is the height of the cylinder.
3. Spheres
Spheres, perfectly symmetrical three-dimensional shapes, use the following formula:
Volume = (4/3) × π × radius³
This formula highlights the cubic relationship between radius and volume; a small increase in radius leads to a significant increase in volume.
4. Cones
Cones, with their circular base tapering to a point, require this formula:
Volume = (1/3) × π × radius² × height
Notice the (1/3) factor, reflecting that a cone occupies only one-third of the volume of a cylinder with the same base and height.
5. Pyramids
Pyramids, with their polygonal base and apex, have a volume formula that depends on the area of the base:
Volume = (1/3) × base area × height
The base area will vary depending on the shape of the base (square, rectangle, triangle, etc.).
Irregular Shapes and Displacement Methods
Calculating the volume of irregularly shaped objects is more challenging. Direct measurement using length, width, and height isn't possible. Instead, we rely on the principle of water displacement. This method involves submerging the object in a known volume of water and measuring the increase in water level. The difference in water levels represents the volume of the object.
This method is particularly useful for objects with complex geometries or those that are difficult to measure directly. It's a widely used technique in various scientific and engineering applications.
Applications of Volume Measurement: Across Diverse Fields
The concept of volume finds applications across a wide range of disciplines:
1. Engineering and Architecture
Engineers use volume calculations extensively in designing structures, calculating material quantities, and assessing the capacity of containers. Accurate volume calculations are crucial for ensuring structural integrity and efficient resource allocation. From designing bridges to constructing buildings, volume plays a pivotal role.
2. Medicine and Healthcare
In the medical field, volume measurements are vital for determining dosages of medication, assessing fluid balance in patients, and analyzing the size of organs or tumors. Precise volume calculations are crucial for accurate diagnosis and treatment.
3. Chemistry and Physics
In chemistry, volume is fundamental for understanding concentrations of solutions, carrying out chemical reactions, and analyzing chemical properties. In physics, volume is essential for understanding fluid dynamics, thermodynamics, and other areas involving the behavior of matter.
4. Environmental Science
Volume calculations are essential for understanding water resource management, assessing pollution levels, and predicting the impact of environmental changes. Volume estimations play a key role in modelling environmental processes.
5. Everyday Life
Even in everyday life, understanding volume is important. From cooking (measuring ingredients) to shopping (purchasing liquids or gases), volume is a constant consideration.
Advanced Concepts in Volume: Beyond Basic Shapes
Beyond the basic geometrical shapes, the calculation of volume can become significantly more complex. For example:
- Calculus: For irregularly shaped objects that cannot be easily described by simple geometric formulas, calculus provides the tools to calculate volumes through integration. This involves breaking down the object into infinitesimally small volumes and summing them up.
- Solid Modeling: Computer-aided design (CAD) software uses solid modeling techniques to represent three-dimensional objects digitally. This allows for precise volume calculations even for complex, irregular shapes.
- Fractals: The concept of volume also extends to fractal geometry, where objects exhibit self-similarity at different scales. Calculating the volume of fractal objects requires specialized mathematical approaches.
Conclusion: The Ubiquity of Volume
The amount of space an object occupies, its volume, is a foundational concept with far-reaching implications. From simple geometric shapes to complex, irregular forms, understanding how to calculate and apply volume measurements is essential across numerous scientific, engineering, and everyday contexts. Mastering the concepts and techniques presented in this guide will equip you with the knowledge to tackle a broad range of volume-related challenges. Further exploration into advanced techniques like calculus and solid modeling will unlock even deeper insights into the fascinating world of three-dimensional measurement.
Latest Posts
Latest Posts
-
Find The Area Of A Shaded Triangle
Apr 02, 2025
-
Which Of The Following Would Decrease Glomerular Filtration Rate
Apr 02, 2025
-
The Slope Of Speed Time Graph Indicates
Apr 02, 2025
-
What Is The Approximate Size Of A Nucleus
Apr 02, 2025
-
Hydrogen Peroxide Catalyzed By Manganese Dioxide
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about The Amount Of Space An Object Occupies . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
