Find The Area Of A Shaded Triangle
News Leon
Apr 02, 2025 · 5 min read
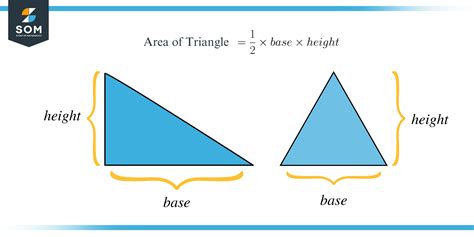
Table of Contents
Finding the Area of a Shaded Triangle: A Comprehensive Guide
Finding the area of a shaded triangle can seem daunting at first, but with a systematic approach and understanding of geometric principles, it becomes a manageable task. This comprehensive guide will equip you with the knowledge and techniques to solve a wide range of problems involving shaded triangles, regardless of their complexity. We'll explore various methods, from simple formulas to more advanced techniques involving coordinate geometry and trigonometry. Let's dive in!
Understanding the Basics: Area of a Triangle
Before tackling shaded triangles, let's refresh our understanding of the fundamental formula for the area of a triangle:
Area = (1/2) * base * height
This formula is applicable to all triangles, regardless of their shape or orientation. The base is any side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex.
Identifying the Base and Height
The key to finding the area of any triangle lies in correctly identifying its base and height. Sometimes, this is straightforward; other times, it requires a bit more detective work.
-
Right-angled triangles: In right-angled triangles, one leg can be considered the base, and the other leg serves as the height.
-
Other triangles: For non-right-angled triangles, the height is the perpendicular line drawn from a vertex to the opposite side (the base). This perpendicular line can fall inside or outside the triangle, depending on the triangle's shape.
Methods for Finding the Area of Shaded Triangles
Shaded triangles often appear within larger shapes, making the identification of their base and height less obvious. Let's explore several common scenarios and strategies:
1. Using Subtraction: The "Whole Minus Parts" Method
This is a powerful technique, especially when the shaded triangle is part of a larger shape with a known area.
Steps:
-
Find the area of the larger shape: This could be a rectangle, square, trapezoid, or another polygon, encompassing the shaded triangle. Use the appropriate formula for the area of that shape.
-
Find the area of the unshaded parts: Identify the unshaded regions within the larger shape. These are often triangles or other polygons whose areas can be calculated individually.
-
Subtract the unshaded areas from the total area: The difference represents the area of the shaded triangle.
Example: A rectangle with dimensions 10 cm by 8 cm contains a shaded triangle. Two unshaded right-angled triangles have areas of 12 cm² and 18 cm². The rectangle's area is 10 * 8 = 80 cm². The shaded triangle's area is 80 - 12 - 18 = 50 cm².
2. Using Coordinate Geometry
If the vertices of the shaded triangle are given as coordinates on a Cartesian plane, we can employ the determinant formula to calculate the area. This method is particularly useful when dealing with irregular shapes.
The Determinant Formula:
For a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃), the area is given by:
Area = (1/2) |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|
Remember to take the absolute value to ensure a positive area.
3. Using Trigonometry: The Sine Rule
When the lengths of two sides and the included angle of the shaded triangle are known, we can utilize the sine rule to find the area.
The Sine Rule for Area:
Area = (1/2) * a * b * sin(C)
Where 'a' and 'b' are the lengths of two sides, and 'C' is the angle between them.
4. Breaking Down Complex Shapes
Complex shaded triangles might require a more strategic approach. Break down the larger shape into smaller, simpler triangles whose areas you can calculate using the basic formula or other methods. Sum the areas of these smaller triangles to find the area of the shaded region.
Advanced Techniques and Challenging Scenarios
Let's delve into some more challenging scenarios and the techniques to solve them:
Shaded Triangles within Circles
Finding the area of a shaded triangle inscribed in a circle often involves using the properties of circles and triangles. This might include utilizing the circle's radius, the triangle's angles, or the lengths of its sides. Remember to utilize trigonometric functions such as sine and cosine to relate angles and sides.
Shaded Triangles with Irregular Boundaries
If the shaded triangle has curved or irregular boundaries, using integration techniques from calculus can be necessary. This involves dividing the shaded area into infinitesimally small strips and summing their areas using integral calculus. This is a more advanced method requiring a strong mathematical foundation.
Overlapping Triangles
When dealing with overlapping triangles, carefully identify the overlapping region and subtract it from the total area of the individual triangles to find the area of the shaded portion.
Practical Applications
The ability to find the area of a shaded triangle has numerous practical applications:
-
Engineering and Architecture: Calculating areas for construction materials, structural design, and land surveying.
-
Computer Graphics: Generating realistic images and models.
-
Cartography: Measuring areas on maps and geographical data.
-
Physics and Engineering: Solving problems related to forces, moments, and centers of mass.
Conclusion: Mastering the Art of Finding Shaded Triangle Areas
Finding the area of a shaded triangle might initially seem complex, but by understanding the fundamental principles of geometry, utilizing the appropriate formulas and techniques, and employing a systematic approach, you can master this crucial skill. Remember that choosing the right method depends entirely on the given information and the shape of the shaded triangle. Practice is key—the more problems you solve, the more comfortable and confident you'll become in tackling even the most challenging scenarios. By mastering this skill, you'll open doors to a deeper understanding of geometric problems and their practical applications.
Latest Posts
Latest Posts
-
What Is The Overall Tone Of This Passage
Apr 03, 2025
-
The Mass Of A Mole Of Nacl Is The
Apr 03, 2025
-
Desktop Is A Computer Term Which Refers To
Apr 03, 2025
-
Which Of The Esters Cannot Undergo Claisen Self Condensation
Apr 03, 2025
-
1 A 2 X 2 Integral Formula
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of A Shaded Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
