The Slope Of Speed Time Graph Indicates
News Leon
Apr 02, 2025 · 6 min read
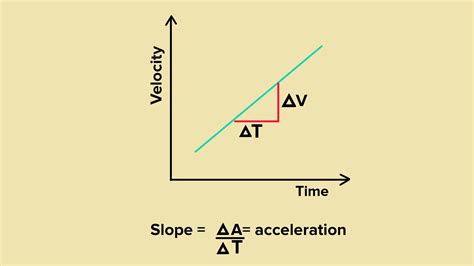
Table of Contents
The Slope of a Speed-Time Graph Indicates: A Comprehensive Guide
The speed-time graph, also known as a velocity-time graph, is a fundamental tool in physics and kinematics used to visualize and analyze the motion of an object. Understanding how to interpret this graph, particularly the significance of its slope, is crucial for comprehending concepts like acceleration, deceleration, and constant velocity. This article will delve deep into the meaning of the slope of a speed-time graph, providing detailed explanations, examples, and practical applications.
Understanding the Basics: Speed, Time, and Graphs
Before we dive into the intricacies of the slope, let's establish a clear understanding of the elements involved:
- Speed: This refers to the rate at which an object covers distance. It's a scalar quantity, meaning it only has magnitude (e.g., 10 m/s).
- Time: The duration of the motion or the interval over which the speed is measured.
- Speed-Time Graph: A graph where the x-axis represents time and the y-axis represents speed. Each point on the graph represents the object's speed at a particular time.
The graph itself offers a powerful visual representation of motion. A straight horizontal line indicates constant speed, while a curved line implies changing speed. But it's the slope of the line that holds the key to understanding the object's acceleration.
The Slope: The Key to Understanding Acceleration
The slope of a speed-time graph represents the acceleration of the object. Remember, acceleration is the rate of change of velocity (which includes both speed and direction). In the context of a speed-time graph (where we are focusing on speed, the magnitude of velocity), a positive slope indicates acceleration (speeding up), a negative slope indicates deceleration (slowing down), and a zero slope indicates constant speed (no acceleration).
Calculating Acceleration from the Slope
The slope of any line is calculated by dividing the change in the y-axis value by the change in the x-axis value. In a speed-time graph:
Acceleration = (Change in Speed) / (Change in Time)
This can also be expressed as:
Acceleration = (Final Speed - Initial Speed) / (Final Time - Initial Time)
Units: The units of acceleration depend on the units used for speed and time. If speed is measured in meters per second (m/s) and time in seconds (s), then the unit of acceleration will be meters per second squared (m/s²).
Interpreting Different Slopes
Let's examine the different scenarios presented by varying slopes on a speed-time graph:
-
Positive Slope (Upward sloping line): This indicates positive acceleration, meaning the object is speeding up. The steeper the slope, the greater the acceleration.
-
Negative Slope (Downward sloping line): This indicates negative acceleration or deceleration, meaning the object is slowing down. The steeper the slope (downwards), the greater the deceleration.
-
Zero Slope (Horizontal line): This indicates zero acceleration, meaning the object is moving at a constant speed. There's no change in speed over time.
-
Curved Line: A curved line on a speed-time graph indicates a changing acceleration. The acceleration itself is not constant; it's increasing or decreasing. The slope of the tangent to the curve at any point gives the instantaneous acceleration at that specific moment.
Real-World Applications and Examples
The concepts discussed above are not merely theoretical exercises. They have numerous real-world applications:
1. Analyzing Vehicle Motion
Speed-time graphs are extensively used in analyzing the motion of vehicles. For example, traffic accident investigators can use data from a vehicle's black box to create a speed-time graph. The slope of the graph will reveal crucial information about the vehicle's acceleration and deceleration before and during the accident, assisting in the reconstruction of events.
This analysis can help determine factors contributing to the accident, such as excessive speed, sudden braking, or improper acceleration. The data can be used to support claims, determine liability, and inform future safety measures.
2. Studying Projectile Motion
In the study of projectile motion, the speed-time graph helps to visualize the changes in speed of an object launched into the air. The upward portion of the graph (positive slope) shows the deceleration due to gravity, while the downward portion (negative slope) shows acceleration due to gravity. The point where the slope is zero represents the peak of the projectile's trajectory, where its vertical speed is momentarily zero before it begins to fall.
3. Analyzing Free Fall
Free fall is the motion of an object under the influence of gravity alone. A speed-time graph of an object in free fall will show a constant positive slope (assuming downward motion is considered positive), indicating a constant acceleration due to gravity (approximately 9.8 m/s² on Earth). Air resistance is often ignored in idealized free-fall scenarios, but its effects can be seen in real-world experiments where the slope may not be perfectly constant.
4. Understanding Simple Harmonic Motion (SHM)
In SHM, like that of a pendulum or a mass on a spring, the speed varies periodically. The speed-time graph will be sinusoidal, with the slope changing continuously. The maximum slope indicates maximum acceleration, which occurs at the points of maximum displacement from equilibrium.
5. Designing and Optimizing Machines
Engineers utilize speed-time graphs to analyze the performance of machines and mechanical systems. By plotting the speed of different components over time, engineers can identify areas where acceleration or deceleration might be inefficient or lead to wear and tear. Optimizing these aspects can improve energy efficiency and extend the lifespan of the machine.
Advanced Concepts: Instantaneous and Average Acceleration
While the slope provides a clear indication of acceleration, it's important to differentiate between average and instantaneous acceleration:
-
Average Acceleration: This represents the overall change in speed over a specific time interval. It's the slope of the secant line connecting two points on the speed-time graph.
-
Instantaneous Acceleration: This represents the acceleration at a single point in time. It's the slope of the tangent line to the curve at that specific point. For a curved speed-time graph, the instantaneous acceleration changes continuously.
Conclusion: The Power of Visual Representation
The speed-time graph provides a powerful visual representation of an object's motion. The slope of the graph is a critical element, directly indicating the object's acceleration. Understanding the significance of positive, negative, and zero slopes allows for a deeper comprehension of motion, enabling analysis of various scenarios from vehicle accidents to projectile motion and beyond. By mastering the interpretation of speed-time graphs, one can gain valuable insights into the dynamics of moving objects and apply this knowledge to diverse fields of science and engineering. The ability to calculate and interpret acceleration from a speed-time graph is a fundamental skill for anyone studying physics or related disciplines. Remember that while this article provides a detailed explanation, practice is key to mastering this concept and its practical applications.
Latest Posts
Latest Posts
-
What Is The Overall Tone Of This Passage
Apr 03, 2025
-
The Mass Of A Mole Of Nacl Is The
Apr 03, 2025
-
Desktop Is A Computer Term Which Refers To
Apr 03, 2025
-
Which Of The Esters Cannot Undergo Claisen Self Condensation
Apr 03, 2025
-
1 A 2 X 2 Integral Formula
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about The Slope Of Speed Time Graph Indicates . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
