Part Of Line With Two Endpoints
News Leon
Mar 29, 2025 · 6 min read
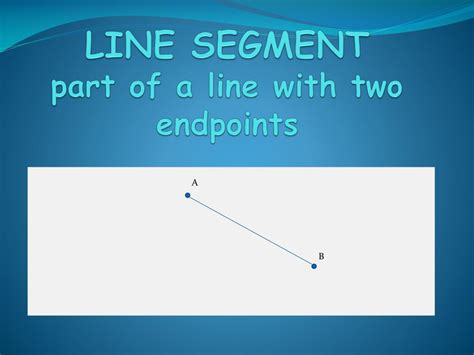
Table of Contents
Part of a Line: Exploring Line Segments and Their Properties
A line, in its purest geometric form, stretches infinitely in both directions. However, the real world rarely deals with such boundless entities. More often, we encounter parts of lines – specifically, line segments. Understanding line segments, their properties, and their applications is crucial in various fields, from basic geometry to advanced calculus and computer graphics. This comprehensive guide delves deep into the world of line segments, exploring their definition, properties, and applications.
Defining a Line Segment
A line segment is a part of a line that is bounded by two distinct endpoints. Unlike a line, which extends infinitely, a line segment has a definite beginning and end. This finite nature makes it a much more practical concept to work with in real-world scenarios. We can represent a line segment using its endpoints. For instance, if we have two points, A and B, the line segment connecting them is denoted as AB or BA. The order of the letters doesn't change the segment itself, only the direction in which we consider it.
Key Properties of Line Segments
Several key properties define and distinguish line segments from other geometric figures:
1. Finite Length:
The most defining characteristic of a line segment is its finite length. This length can be measured and expressed numerically. The length of a line segment AB is often denoted as |AB| or simply AB. Calculating this length depends on the coordinate system used; in a Cartesian plane, the distance formula is employed.
2. Defined Endpoints:
Line segments are uniquely defined by their two endpoints. These endpoints are essential for determining the segment's length and location. Knowing the coordinates of the endpoints allows for precise geometric calculations and manipulations.
3. Collinearity:
All points constituting a line segment are collinear, meaning they lie on the same straight line. This collinearity is a fundamental property that distinguishes line segments from curves or other non-linear geometric shapes.
4. Sub-segments:
A line segment can be divided into smaller sub-segments. For example, a point C lying on the line segment AB divides it into two smaller segments AC and CB. The lengths of these sub-segments add up to the length of the original segment (AC + CB = AB). This property is crucial for various geometric constructions and proofs.
5. Midpoint:
Every line segment has a unique midpoint, which divides the segment into two equal halves. The midpoint's coordinates can be easily calculated using the coordinates of the endpoints. If A = (x₁, y₁) and B = (x₂, y₂), then the midpoint M has coordinates ((x₁ + x₂)/2, (y₁ + y₂)/2).
Measuring the Length of a Line Segment
The method for measuring the length of a line segment depends on the context.
In a Cartesian Coordinate System:
In a two-dimensional Cartesian coordinate system, the distance formula is used to calculate the length of a line segment. If the endpoints A and B have coordinates (x₁, y₁) and (x₂, y₂) respectively, then the length of the line segment AB is given by:
AB = √[(x₂ - x₁)² + (y₂ - y₁)²]
This formula is derived from the Pythagorean theorem, treating the line segment as the hypotenuse of a right-angled triangle.
In a Three-Dimensional Cartesian Coordinate System:
Extending this to three dimensions, if A = (x₁, y₁, z₁) and B = (x₂, y₂, z₂), then the length is:
AB = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
This generalization maintains the core principle of using the Pythagorean theorem in higher dimensions.
Using Geometric Tools:
In practical scenarios, the length of a line segment can be measured using physical tools like rulers, calipers, or measuring tapes. These tools provide direct measurements, useful when dealing with physical objects.
Applications of Line Segments
Line segments are fundamental building blocks in various fields. Here are a few examples:
1. Geometry:
Line segments are essential in various geometric constructions, such as creating triangles, quadrilaterals, and other polygons. They form the edges of these shapes, allowing for the study of their properties and relationships.
2. Computer Graphics:
In computer graphics, line segments are used to represent edges of objects. They are the fundamental primitives used in drawing lines, polygons, and other shapes on the screen. Algorithms for rendering and manipulating images extensively utilize line segment properties and calculations. For example, line clipping algorithms determine which parts of a line segment are visible within a specified viewing area.
3. Vector Graphics:
Vector graphics software relies heavily on line segments to define shapes. These shapes are mathematically defined by their vertices (endpoints of line segments), enabling scalable and resolution-independent graphics.
4. Engineering and Surveying:
In engineering and surveying, line segments are used to represent distances and directions. They are crucial for planning constructions, measuring land, and creating accurate maps. Surveyors use measuring tools to determine the lengths and orientations of line segments to define boundaries and plot locations.
5. Physics:
Line segments represent vectors in physics. Vectors have both magnitude (length) and direction, making line segments ideal for representing forces, velocities, and other physical quantities. Calculations involving vectors utilize the properties of line segments extensively.
6. Linear Algebra:
In linear algebra, vectors are frequently represented by line segments originating from the origin. The operations on these vectors, such as addition and scalar multiplication, are inherently linked to the geometric properties of line segments.
Advanced Concepts Related to Line Segments
Beyond the basics, several advanced concepts relate to line segments:
1. Perpendicular Bisector:
The perpendicular bisector of a line segment is a line that is perpendicular to the segment and passes through its midpoint. This line is equidistant from both endpoints of the segment.
2. Angle Bisector:
When two line segments intersect to form an angle, the angle bisector is a line segment that divides the angle into two equal parts.
3. Concurrent Lines:
Several line segments can be concurrent, meaning they intersect at a single point. This point is often significant in the geometric properties of the involved shapes.
Line Segments vs. Rays and Lines
It's important to differentiate between line segments, rays, and lines:
- Line: Extends infinitely in both directions.
- Ray: Has one endpoint and extends infinitely in one direction.
- Line Segment: Has two endpoints and is finite in length.
These distinctions are crucial for precise geometric definitions and calculations.
Conclusion
Line segments, despite their seemingly simple definition, are fundamental geometric objects with far-reaching applications. Understanding their properties, including their finite length, defined endpoints, and collinearity, is essential for various fields. From basic geometric constructions to advanced computer graphics and engineering applications, line segments remain an indispensable tool in mathematics and related disciplines. Mastering the concepts and calculations related to line segments provides a solid foundation for tackling more complex geometric problems and applications. This knowledge equips individuals with the skills to analyze, interpret, and manipulate geometric shapes effectively, benefiting both theoretical understanding and practical problem-solving.
Latest Posts
Latest Posts
-
Which Of The Following Is True About Monopolistic Competition
Apr 01, 2025
-
Which Of The Following Is The Site Of Translation
Apr 01, 2025
-
What Is The Atomic Number Of An Atom Equal To
Apr 01, 2025
-
Parathyroid Hormone Does All Of The Following Except
Apr 01, 2025
-
Which Structure Is Not Part Of A Neuron
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Part Of Line With Two Endpoints . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
