Number Of Atoms In A Simple Cubic Unit Cell
News Leon
Apr 02, 2025 · 5 min read
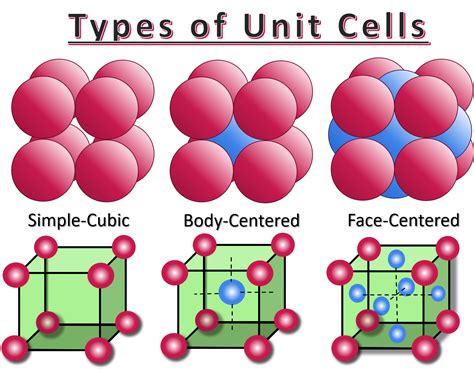
Table of Contents
The Number of Atoms in a Simple Cubic Unit Cell: A Deep Dive into Crystallography
Understanding the number of atoms within a unit cell is fundamental to comprehending crystal structures and their properties. This article delves into the intricacies of calculating the number of atoms in a simple cubic (SC) unit cell, providing a comprehensive explanation accessible to both beginners and those with some prior knowledge of crystallography. We will explore the underlying concepts, address common misconceptions, and examine the implications of this calculation for various material properties.
What is a Unit Cell?
Before we dive into the atom count, let's establish a clear understanding of what a unit cell is. In crystallography, a unit cell is the smallest repeating unit of a crystal lattice. Imagine a crystal as a three-dimensional array of atoms, ions, or molecules arranged in a highly ordered and periodic manner. The unit cell acts as a blueprint, replicating itself in all directions to build the entire crystal structure.
There are several types of unit cells, classified according to their symmetry and the arrangement of lattice points within them. The simplest of these is the simple cubic (SC) unit cell.
Visualizing the Simple Cubic Unit Cell
The simple cubic unit cell is characterized by its cubic shape and the location of its lattice points. Lattice points represent the positions of atoms (or ions/molecules) within the crystal structure. In an SC unit cell, lattice points are located only at the corners of the cube.
Imagine a cube. Now place a single atom at each of the eight corners. This represents a simple cubic unit cell. It's crucial to remember that these corner atoms are shared between adjacent unit cells. This sharing is key to accurately determining the number of atoms within a single unit cell.
Calculating the Number of Atoms in a Simple Cubic Unit Cell
The key to accurately calculating the number of atoms in an SC unit cell lies in understanding the concept of atom sharing. Each corner atom is shared by eight adjacent unit cells. Therefore, only ⅛ of each corner atom is considered to be within a single unit cell.
Since there are eight corners in a cube, the total number of atoms within a simple cubic unit cell is:
(1/8 atom/corner) * 8 corners = 1 atom
Therefore, a simple cubic unit cell contains one atom.
Beyond the Simple Count: Implications and Applications
While the calculation itself seems straightforward, understanding its implications is crucial for comprehending various material properties. The number of atoms per unit cell directly influences:
-
Density: The density of a crystalline material is directly proportional to the number of atoms per unit cell and inversely proportional to the volume of the unit cell. A higher number of atoms per unit cell generally leads to a higher density (all else being equal).
-
Packing Efficiency: Packing efficiency describes how effectively the atoms fill the available space within the unit cell. The simple cubic structure has a relatively low packing efficiency (52%), meaning there's significant empty space between atoms. This impacts properties like strength and conductivity.
-
Coordination Number: The coordination number represents the number of nearest-neighbor atoms surrounding a central atom. In a simple cubic structure, the coordination number is six, indicating that each atom is surrounded by six other atoms.
-
Crystallographic Properties: The simple cubic structure dictates various crystallographic properties, such as cleavage planes, slip systems (important for ductility), and diffraction patterns. These are observable through techniques such as X-ray diffraction.
Common Misconceptions and Clarifications
A common misconception is to simply count the eight atoms at the corners and conclude there are eight atoms per unit cell. This is incorrect because it fails to account for atom sharing between neighboring unit cells. Always remember to consider the fraction of each atom that resides within the unit cell's boundaries.
Another misconception relates to the visual representation. While diagrams often show atoms as large spheres, it's crucial to remember that these are simplified representations; the atoms are not truly touching. The space between atoms contributes significantly to the overall volume and packing efficiency.
Comparing Simple Cubic to Other Unit Cells
The simple cubic structure is the most basic type of unit cell. However, many materials crystallize in more complex structures, such as:
-
Body-centered cubic (BCC): In addition to corner atoms, a BCC unit cell contains an atom at the center of the cube. This increases the number of atoms per unit cell to two.
-
Face-centered cubic (FCC): An FCC unit cell has atoms at each corner and at the center of each of the six faces. This results in a total of four atoms per unit cell. FCC structures are very common and exhibit higher packing efficiency (74%) than SC.
Understanding the differences in atom arrangements and numbers per unit cell is essential for comparing and contrasting the properties of materials with different crystal structures.
Advanced Considerations and Further Exploration
The discussion above provides a fundamental understanding of the number of atoms in a simple cubic unit cell. However, more advanced concepts can be explored:
-
Basis: The concept of a basis extends the understanding of unit cells beyond just the lattice points. A basis refers to the group of atoms associated with each lattice point. In our simple case, the basis is a single atom. However, more complex structures may have multiple atoms per basis.
-
Bravais Lattices: The 14 Bravais lattices provide a complete classification of all possible three-dimensional lattice arrangements. The simple cubic structure is one of these 14.
-
X-ray Diffraction: X-ray diffraction techniques are instrumental in determining the crystal structure and confirming the number of atoms per unit cell.
Conclusion: A Fundamental Building Block
The seemingly simple calculation of the number of atoms in a simple cubic unit cell serves as a fundamental building block for understanding more complex crystal structures and material properties. Mastering this concept is crucial for anyone pursuing studies in materials science, chemistry, physics, or engineering. By understanding the intricacies of atom sharing and the implications of unit cell structure, we unlock a deeper appreciation for the microscopic world that governs the macroscopic properties of materials. Remember that while the SC unit cell is simple, its principles are essential for understanding more complex crystal systems. This knowledge provides a solid foundation for further exploration into the fascinating world of crystallography and materials science.
Latest Posts
Latest Posts
-
Determine Whether The Following Statement Is True Or False
Apr 03, 2025
-
Is C A Metal Or Nonmetal
Apr 03, 2025
-
Is Coal Igneous Sedimentary Or Metamorphic
Apr 03, 2025
-
What Is The Area Of The Shaded Triangle
Apr 03, 2025
-
Which Of The Following Is Not A Secondary Sex Characteristic
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Number Of Atoms In A Simple Cubic Unit Cell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
