What Is The Area Of The Shaded Triangle
News Leon
Apr 03, 2025 · 5 min read
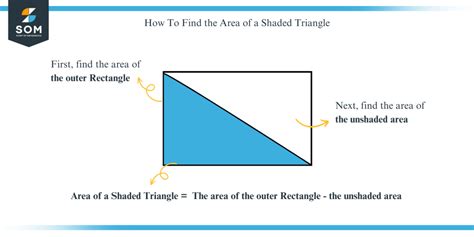
Table of Contents
What is the Area of the Shaded Triangle? A Comprehensive Guide
Determining the area of a shaded triangle can seem deceptively simple, but the approach depends heavily on the context of the problem. This comprehensive guide explores various scenarios, providing step-by-step solutions and highlighting key geometrical concepts. We'll cover methods applicable to triangles embedded within squares, rectangles, circles, and other shapes, employing different formulas and techniques to find the solution.
Understanding the Fundamentals: Area of a Triangle
Before tackling shaded triangles, let's solidify our understanding of the fundamental formula:
Area of a Triangle = (1/2) * base * height
Where:
- Base: The length of one side of the triangle.
- Height: The perpendicular distance from the base to the opposite vertex (the highest point).
This simple formula is the cornerstone of many solutions, but finding the correct base and height in complex scenarios requires careful observation and geometric reasoning.
Scenario 1: Triangle within a Square or Rectangle
Imagine a square or rectangle with a shaded triangle occupying part of it. The easiest cases involve a triangle that shares a side with the square or rectangle. In these instances, one side of the square or rectangle conveniently serves as the base of the triangle.
Example: A square with side length 10cm has a triangle shaded within it. The triangle shares one of the square's sides as its base, and the height of the triangle is also 10cm.
Solution:
- Identify the base: The base of the triangle is 10cm (one side of the square).
- Identify the height: The height of the triangle is 10cm (the same as the side length of the square).
- Apply the formula: Area = (1/2) * 10cm * 10cm = 50cm²
More Complex Scenarios:
If the triangle is not aligned with the sides of the rectangle or square, you might need to break it down into smaller, easily solvable triangles, or use other techniques, such as coordinate geometry. For instance, if the vertices of the shaded triangle are given as coordinates, you can use the determinant formula for the area of a triangle given its vertices.
Let's say the vertices are (x1, y1), (x2, y2), and (x3, y3). The area is:
Area = (1/2) | x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) |
Scenario 2: Triangle within a Circle
Finding the area of a shaded triangle inscribed within a circle is more challenging. The solution depends on the type of triangle. For example, if it's an equilateral triangle inscribed in a circle with a known radius, we can use trigonometry to find the side length and subsequently the area.
Example: An equilateral triangle is inscribed within a circle of radius 'r'.
Solution:
- Equilateral Triangle Properties: The height of an equilateral triangle is (√3/2) * side length. The radius of the circumscribed circle is (2/3) * height.
- Relate Radius and Height: We know 'r' (radius). Therefore, the height of the triangle is (3/2)r.
- Find Side Length: Using the height formula for an equilateral triangle, solve for the side length: side = (2/√3) * height = (2/√3) * (3/2)r = √3r
- Calculate Area: Area = (1/2) * base * height = (1/2) * √3r * (3/2)r = (3√3/4)r²
Scenario 3: Overlapping Triangles
Situations involving overlapping triangles require careful subtraction of areas.
Example: Two triangles overlap, forming a shaded region. We know the area of each individual triangle and the area of the overlapping region. Find the area of the shaded region (the combined area of the non-overlapping portions).
Solution:
- Individual Areas: Calculate the areas of the two triangles separately.
- Overlapping Area: Subtract the area of the overlapping region from the sum of the individual areas.
The result is the area of the shaded region.
Scenario 4: Using Trigonometry
Triangles within other geometric shapes often require trigonometric functions to find missing sides or angles. Knowing the angles of a triangle and one side allows for the use of the sine rule or cosine rule to find other sides, enabling the area calculation.
Example: A triangle is inscribed in a sector of a circle. The radius and the central angle are known.
Solution:
- Find Side Lengths: Use trigonometry to find the lengths of the sides of the triangle, often using the sine and cosine rules.
- Calculate Area: Use the standard area formula (1/2 * base * height) once the base and height are known.
Scenario 5: Complex Polygons and Subdivision
Sometimes, the shaded triangle is part of a more complex polygon. In such cases, subdividing the polygon into smaller, simpler shapes (including the shaded triangle) is often the best strategy.
Example: A shaded triangle is part of a hexagon.
Solution:
- Subdivision: Divide the hexagon into smaller triangles and other shapes.
- Individual Areas: Calculate the areas of the smaller shapes.
- Subtraction (if necessary): Subtract the areas of the unwanted shapes from the total area of the hexagon to isolate the area of the shaded triangle.
Scenario 6: Coordinate Geometry
When the vertices of the shaded triangle are given as coordinates (x,y) in a Cartesian plane, we can use the determinant method or other techniques of coordinate geometry. The determinant method, already mentioned above, is a powerful and efficient way to find the area, especially when dealing with non-right angled triangles.
Advanced Techniques and Considerations
For highly complex situations, advanced techniques such as calculus (integration) might be necessary. These techniques are typically applied to scenarios involving curves or irregularly shaped regions where the traditional base and height method becomes impractical. Numerical methods might also be used for approximations in such situations.
Conclusion: A Multifaceted Problem
Determining the area of a shaded triangle is not a single-solution problem. The approach is highly dependent on the context and the given information. Mastering this requires a solid foundation in geometry, trigonometry, and sometimes, calculus. By systematically analyzing the problem, identifying relevant properties, and choosing the appropriate method, you can successfully solve even the most challenging shaded triangle area problems. Remember to always draw a clear diagram, label all known values, and carefully consider which method best suits the given information. Practice makes perfect, so work through many examples to build your skills and confidence in tackling these types of problems.
Latest Posts
Latest Posts
-
Paleolithic Age Is Also Known As The
Apr 04, 2025
-
What Is Found In Both Eukaryotic And Prokaryotic Cells
Apr 04, 2025
-
Select The Correct Electron Configuration For Cr
Apr 04, 2025
-
Can A Pure Substance Be A Compound
Apr 04, 2025
-
3 Types Of Winds Class 7
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of The Shaded Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
