List One Way A Parallelogram And A Rhombus Are Different
News Leon
Apr 05, 2025 · 5 min read
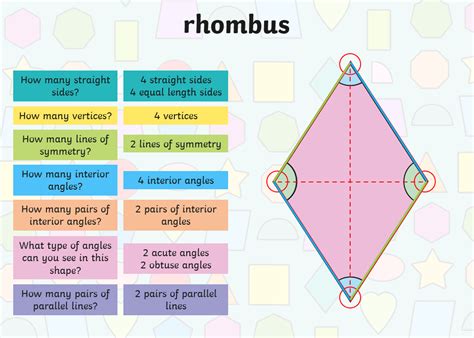
Table of Contents
One Key Difference: Parallelogram vs. Rhombus
Parallelograms and rhombuses are both fascinating shapes in the world of geometry, belonging to the broader family of quadrilaterals. While they share some similarities, understanding their key differences is crucial for anyone studying geometry, from high school students to advanced mathematicians. This article dives deep into the subtle yet significant distinctions between these two shapes, focusing on one primary difference that sets them apart. We'll also explore related concepts to ensure a comprehensive understanding.
The Defining Difference: Angles vs. Sides
The most fundamental difference between a parallelogram and a rhombus lies in their angles and sides. While both are quadrilaterals with opposite sides parallel, a rhombus possesses an additional constraint: all four sides must be of equal length. A parallelogram, on the other hand, only requires opposite sides to be equal in length; adjacent sides can have different lengths. This seemingly small distinction leads to significant geometrical consequences.
This core difference can be summarized concisely as follows:
- Parallelogram: Opposite sides are parallel and equal in length. Adjacent sides may or may not be equal in length. Angles may or may not be equal.
- Rhombus: All four sides are equal in length. Opposite sides are parallel. Adjacent angles are supplementary (add up to 180 degrees).
Visualizing the Difference
Imagine two quadrilaterals. One is a rectangle – a classic example of a parallelogram with four right angles and opposite sides equal. The other is a square, tilted slightly. The rectangle’s adjacent sides are clearly different in length, while the tilted square (a rhombus) has all four sides equal. This perfectly illustrates the core difference.
The implications of this core difference are far-reaching, impacting several geometrical properties. Let's explore these further.
Exploring Related Properties
1. Angle Properties:
-
Parallelogram: Opposite angles are equal. Adjacent angles are supplementary (add up to 180°). However, the individual angles themselves can have various measures, not necessarily being equal. Think of a rectangle – its angles are all 90°, while a slanted parallelogram will have a mix of acute and obtuse angles.
-
Rhombus: In addition to the properties of a parallelogram (opposite angles equal, adjacent angles supplementary), a rhombus has the added characteristic that adjacent angles are supplementary. This arises directly from the equal side lengths and the parallel sides. This supplementary angle relationship is not a guaranteed property of all parallelograms.
2. Diagonals:
-
Parallelogram: The diagonals of a parallelogram bisect each other. This means they intersect at their midpoints, dividing each diagonal into two equal segments. However, the diagonals are generally not equal in length.
-
Rhombus: The diagonals of a rhombus also bisect each other (a property inherited from being a parallelogram). Furthermore, the diagonals of a rhombus are perpendicular to each other, intersecting at a 90° angle. This perpendicularity is a defining characteristic of a rhombus, not shared by all parallelograms. Additionally, the diagonals of a rhombus bisect the angles of the rhombus. This means each diagonal divides a pair of opposite angles into two equal halves.
3. Area Calculation:
-
Parallelogram: The area of a parallelogram is calculated using the formula: Area = base × height. The base is the length of one side, and the height is the perpendicular distance between that base and the opposite side.
-
Rhombus: Since a rhombus is a special type of parallelogram, the same basic formula applies (Area = base × height). However, for a rhombus, there's an alternative and equally valid formula: Area = (1/2) × d1 × d2, where d1 and d2 are the lengths of the two diagonals. This formula leverages the perpendicularity of the diagonals.
Special Cases and Overlap
It's important to note that there is some overlap between parallelograms and rhombuses. A square, for example, is both a parallelogram and a rhombus. A square satisfies all the properties of both shapes – it has equal sides, parallel opposite sides, and right angles. A square represents the intersection of these two geometrical sets. Similarly, a rectangle is a parallelogram but not a rhombus unless it is a square.
Advanced Concepts and Applications
The differences between parallelograms and rhombuses extend beyond basic geometry. These concepts have implications in:
-
Linear Algebra: Parallelograms and rhombuses find applications in representing vectors and transformations in two-dimensional space. The properties of these shapes directly impact vector operations and matrix representations.
-
Computer Graphics: Understanding the properties of parallelograms and rhombuses is essential in computer graphics for creating and manipulating two-dimensional shapes and textures. Efficient algorithms often rely on these geometrical principles.
-
Physics and Engineering: Parallelogram and rhombus-based structures are frequently used in engineering designs, particularly in situations involving forces and stresses. Understanding their properties is vital for structural analysis and stability calculations.
-
Crystallography: The structure of many crystalline materials can be analyzed using parallelogram and rhombus-based unit cells, reflecting the inherent symmetry and repeating patterns found in solids.
Conclusion: More Than Just Sides
While both parallelograms and rhombuses have parallel opposite sides, the key difference – the equal side length constraint in a rhombus – leads to a cascade of other distinct properties, including perpendicular diagonals, angle bisection by diagonals, and alternative area calculation methods. Understanding this fundamental difference is key to unlocking a deeper appreciation of the rich world of geometrical shapes and their applications across various disciplines. This article provides a firm foundation for further exploration of these fascinating figures and their roles in the broader mathematical landscape. The subtle distinction between their defining characteristics gives rise to significant variations in their other properties, making the comparison between a parallelogram and a rhombus a fascinating exploration within the field of geometry.
Latest Posts
Latest Posts
-
Are Centigrade And Celsius The Same
Apr 05, 2025
-
Difference Between Cls And Self In Python
Apr 05, 2025
-
The Cell Wall In Bacteria Is Primarily Composed Of
Apr 05, 2025
-
What Is 2 3 Repeating As A Fraction
Apr 05, 2025
-
Constant Returns To Scale Production Function
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about List One Way A Parallelogram And A Rhombus Are Different . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
