Constant Returns To Scale Production Function
News Leon
Apr 05, 2025 · 7 min read
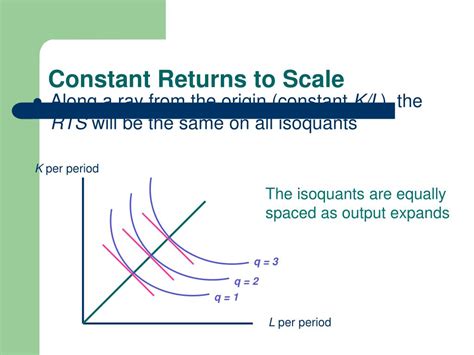
Table of Contents
Constant Returns to Scale Production Function: A Comprehensive Guide
The production function, a cornerstone of economic analysis, describes the relationship between the inputs used in production and the resulting output. Understanding different types of production functions is crucial for businesses to optimize their resource allocation and for economists to model economic growth and development. This article delves into the constant returns to scale (CRS) production function, exploring its definition, properties, implications, and applications. We'll examine its mathematical representation, its contrasting relationship with increasing and decreasing returns to scale, and its relevance in various economic contexts.
Defining Constant Returns to Scale
A production function exhibits constant returns to scale (CRS) if increasing all inputs by a certain proportion leads to an exactly proportional increase in output. In simpler terms, if you double all your inputs, you double your output; if you triple your inputs, you triple your output, and so on. This contrasts with increasing returns to scale (IRS), where output increases more than proportionally to input increases, and decreasing returns to scale (DRS), where output increases less than proportionally to input increases.
Mathematically, a production function, F(K, L), where K represents capital and L represents labor, exhibits CRS if:
F(tK, tL) = tF(K, L) for all t > 0
Where 't' represents the proportional increase in inputs. This equation states that if we multiply both capital (K) and labor (L) by a factor 't', the output will also be multiplied by the same factor 't'.
Examples of Constant Returns to Scale
While perfectly constant returns to scale are rarely observed in the real world due to factors like managerial limitations or indivisibilities of certain inputs, many production processes approximate CRS over a certain range of output. Here are some illustrative examples:
-
Perfectly competitive industries: In a perfectly competitive market with free entry and exit, firms tend to operate under conditions of CRS in the long run. If a firm experiences profits above normal levels, more firms will enter the market, driving down prices and profits back to normal. Conversely, losses lead to firms exiting, until profits again normalize. This adjustment process pushes firms towards a scale where they operate under CRS.
-
Linear production functions: A simple linear production function like Q = aK + bL (where a and b are constants representing the productivity of capital and labor) exhibits CRS. Doubling both K and L will clearly double the output Q.
-
Some agricultural production: In certain agricultural settings, particularly with extensive farming, a doubling of land, seeds, and labor might lead to a near doubling of crop yield. This represents an approximation of CRS.
Distinguishing CRS from IRS and DRS
Understanding the distinctions between CRS, IRS, and DRS is crucial for making informed business decisions and policy recommendations.
Increasing Returns to Scale (IRS): IRS occurs when a proportional increase in inputs leads to a greater than proportional increase in output. This is often associated with economies of scale, where larger firms can achieve lower average costs due to factors like specialization, bulk purchasing, and technological advancements. Mathematically, F(tK, tL) > tF(K, L) for t > 1.
Decreasing Returns to Scale (DRS): DRS occurs when a proportional increase in inputs leads to a less than proportional increase in output. This often arises from managerial difficulties in coordinating larger operations, diminishing returns to individual factors of production (e.g., overcrowding in a factory), and other limitations. Mathematically, F(tK, tL) < tF(K, L) for t > 1.
| Feature | Constant Returns to Scale (CRS) | Increasing Returns to Scale (IRS) | Decreasing Returns to Scale (DRS) |
|---|---|---|---|
| Input Increase | Proportional | Proportional | Proportional |
| Output Increase | Proportional | More than Proportional | Less than Proportional |
| Average Cost | Constant | Decreasing | Increasing |
| Examples | Competitive industries (long run) | Early stages of a firm's growth | Mature firms, managerial limitations |
Implications of Constant Returns to Scale
The presence of CRS has significant implications for various aspects of the economy:
-
Market Structure: As mentioned earlier, CRS is often associated with perfectly competitive markets in the long run. The free entry and exit of firms push the market towards a state where firms operate at a scale consistent with CRS.
-
Firm Size: Under CRS, there's no inherent advantage to being large or small. Firms can achieve the same average cost regardless of their scale. This contrasts with IRS, where larger firms have a cost advantage, and DRS, where smaller firms have an advantage.
-
Economic Growth: Models of economic growth often incorporate assumptions about returns to scale. A CRS production function implies that sustained economic growth requires continuous increases in both capital and labor inputs.
Mathematical Representations and Cobb-Douglas Function
Various mathematical functions can represent CRS production. One of the most commonly used is the Cobb-Douglas production function:
Q = AK^αL^(1-α)
Where:
- Q is the quantity of output
- K is the quantity of capital
- L is the quantity of labor
- A is a constant representing total factor productivity
- α (alpha) is a constant between 0 and 1 representing the output elasticity of capital. (1-α) is the output elasticity of labor.
A Cobb-Douglas function exhibits CRS if, and only if, the exponents of capital and labor sum to 1 (α + (1-α) = 1). In this case, doubling both K and L will precisely double the output Q.
If α + (1-α) > 1, the function displays IRS; if α + (1-α) < 1, it displays DRS.
Limitations and Real-World Considerations
While the concept of CRS provides a useful framework for understanding production, it's important to acknowledge its limitations:
-
Technological Change: The CRS assumption often ignores the impact of technological progress, which can significantly alter the relationship between inputs and outputs. Technological advancements frequently lead to IRS in the short run.
-
External Economies and Diseconomies of Scale: CRS doesn't account for external economies or diseconomies of scale, which arise from factors outside the individual firm. For example, the presence of a skilled labor pool in a region might benefit all firms in that region, leading to external economies of scale.
-
Empirical Evidence: Empirical studies often find that production functions exhibit IRS at low scales of operation and DRS at very high scales. This indicates that CRS may be a reasonable approximation only over a limited range of output.
-
Fixed Inputs: The model simplifies production by considering capital and labor as perfectly adjustable inputs. In reality, some inputs are fixed in the short run, which can impact the returns to scale observed.
Applications and Further Exploration
The concept of CRS has diverse applications across various economic fields:
-
Macroeconomics: Models of economic growth often use CRS production functions to analyze the relationship between capital accumulation, labor growth, and output expansion.
-
Microeconomics: Firms utilize the understanding of returns to scale to make decisions about optimal plant size, investment in capital, and hiring strategies.
-
International Trade: CRS plays a role in analyzing the implications of trade liberalization and the impact of globalization on firm size and industry structure.
-
Development Economics: CRS considerations are crucial in understanding the challenges of economic development, including the role of technology adoption, infrastructure investment, and human capital development.
Further exploration of CRS could involve investigating specific industry applications, analyzing empirical data to estimate production functions, and considering the impact of technological change on the returns to scale observed. A deeper dive into the nuances of the Cobb-Douglas function, its estimation methods, and its limitations within specific contexts also provides fruitful avenues for further study. Finally, comparing the implications of CRS with alternative production function assumptions contributes to a more nuanced understanding of economic phenomena.
This comprehensive guide provides a thorough understanding of constant returns to scale production functions, highlighting their definition, mathematical representation, implications, limitations, and applications across different economic domains. By grasping this concept, both students and professionals can enhance their understanding of economic principles and make more informed decisions in various contexts.
Latest Posts
Latest Posts
-
Which Best Describes The Law Of Independent Assortment
Apr 06, 2025
-
You Should Always Assign The Needs Met Rating Before
Apr 06, 2025
-
Which Is The Most Densely Populated Continent
Apr 06, 2025
-
Average Velocity On Velocity Time Graph
Apr 06, 2025
-
The First Scientist To Observe Cells With A Microscope Was
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Constant Returns To Scale Production Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
