Is Work A Scalar Or A Vector Quantity
News Leon
Apr 04, 2025 · 6 min read
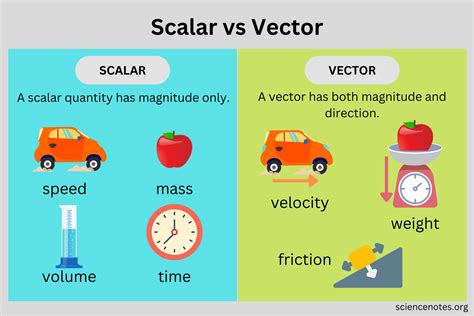
Table of Contents
Is Work a Scalar or a Vector Quantity? A Deep Dive into Physics Concepts
The question of whether work is a scalar or a vector quantity often sparks debate among physics students and enthusiasts. Understanding this requires a solid grasp of the fundamental definitions of scalar and vector quantities, as well as a clear comprehension of the physics behind the concept of work. This article will delve deep into these concepts, offering a comprehensive explanation, addressing common misconceptions, and ultimately answering the question definitively.
Understanding Scalar and Vector Quantities
Before we tackle the main question, let's establish a firm understanding of the difference between scalar and vector quantities.
Scalar Quantities: These are quantities that are fully described by their magnitude (size or amount) alone. They don't have a direction associated with them. Examples include:
- Mass: A 10 kg mass is simply 10 kg, irrespective of direction.
- Temperature: A temperature of 25°C doesn't have a direction.
- Speed: A car moving at 60 km/h has a speed, but no inherent directional component. (Note the distinction between speed and velocity, discussed below).
- Energy: A system possessing 100 Joules of energy simply has that amount of energy, regardless of direction.
Vector Quantities: These quantities are described by both their magnitude and their direction. They require both aspects for complete description. Examples include:
- Displacement: Moving 5 meters east is different from moving 5 meters west. The magnitude (5 meters) and the direction (east or west) are both crucial.
- Velocity: This is the rate of change of displacement. A velocity of 20 m/s north is different from a velocity of 20 m/s south.
- Force: A 10 Newton force applied upwards is different from a 10 Newton force applied downwards.
- Acceleration: The rate of change of velocity, also requiring both magnitude and direction for complete description.
Defining Work in Physics
Work, in the context of physics, is the energy transferred to or from an object via the application of force along a displacement. It's a crucial concept in mechanics and plays a vital role in understanding energy transformations. The crucial point here is the directionality of the force and displacement relative to each other.
The formula for work is often expressed as:
W = Fd cosθ
Where:
- W represents work done
- F represents the magnitude of the force applied
- d represents the magnitude of the displacement
- θ represents the angle between the force vector and the displacement vector.
This formula highlights the importance of the angle θ. It's not simply the product of force and displacement; the component of the force acting in the direction of the displacement is what matters.
Why Work is a Scalar Quantity
Despite the involvement of vectors (force and displacement) in its calculation, work itself is a scalar quantity. This is because the formula incorporates the cosine of the angle between the force and displacement vectors. The cosine function effectively projects the force vector onto the displacement vector, yielding a scalar value representing the component of force doing the work. The result of this calculation – the work done – is a single number representing the energy transferred, without any directional information.
Let's illustrate this with an example:
Imagine pushing a heavy box across a floor. You apply a force at an angle θ to the horizontal. The horizontal component of your force (F cosθ) is what actually moves the box. The vertical component (F sinθ) doesn't contribute to the horizontal displacement. The work done is the product of the horizontal force component and the horizontal displacement. It's a single number representing the energy you expended in moving the box. The direction isn't relevant to the amount of work performed. You did a certain amount of work, regardless of which direction the box moved across the floor.
Addressing Common Misconceptions
Many students struggle with the scalar nature of work because they initially focus on the vector nature of force and displacement. It's important to remember that the calculation of work involves a scalar product (also known as a dot product) of two vectors. The scalar product of two vectors always results in a scalar quantity.
Another misconception stems from the idea that work might have a direction, particularly when dealing with negative work. Negative work simply indicates that the force is acting opposite to the direction of displacement. For example, friction always acts to oppose motion; hence, the work done by friction is always negative. However, the magnitude of the negative work remains a scalar value; it still represents the amount of energy dissipated or transferred, irrespective of its negative sign.
The Role of Work in Energy Transfer and Transformations
Work's scalar nature is intimately linked to its role in energy transfer and transformations. Work represents the amount of energy transferred to or from a system. Energy itself is a scalar quantity; it doesn't have a direction. Therefore, it's logical that the mechanism by which energy is transferred (work) also be a scalar quantity.
The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. Kinetic energy, like energy in general, is a scalar quantity. This further reinforces the scalar nature of work.
Expanding on the Significance of the Angle θ
The cosine of the angle (θ) in the work equation is critical for understanding why work is a scalar. It's not just about multiplying force and displacement; it's about discerning the effective force contributing to the displacement.
- θ = 0°: The force is acting entirely in the direction of displacement. The cosine of 0° is 1, meaning the work done is maximized (W = Fd).
- θ = 90°: The force is perpendicular to the displacement (e.g., carrying a box horizontally). The cosine of 90° is 0, resulting in zero work done. No energy is transferred in the direction of movement, despite the force exerted.
- θ = 180°: The force is directly opposite the displacement (e.g., braking a car). The cosine of 180° is -1, resulting in negative work. This signifies energy being removed from the system.
Conclusion: Work is a Scalar
In conclusion, despite being calculated using vector quantities (force and displacement), work is definitively a scalar quantity. The use of the scalar dot product in its calculation, the inherent nature of energy transfer, and the fact that it only describes the magnitude of energy exchange—without directional information—all point to its scalar classification. Understanding this distinction is crucial for a thorough grasp of fundamental physics concepts and their applications. The angle between force and displacement, incorporated through the cosine function, elegantly resolves the apparent vector conflict and solidifies work's position as a critical scalar quantity in physics.
Latest Posts
Latest Posts
-
What Is Another Name For A Living Thing
Apr 04, 2025
-
Common Neutralizing Materials For Acids Are
Apr 04, 2025
-
Which Of The Following Is A Nonrenewable Energy Source
Apr 04, 2025
-
Electron Dot Structure For Magnesium Oxide
Apr 04, 2025
-
Boiling Point Of Sugar And Water
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Is Work A Scalar Or A Vector Quantity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
