In The Following Figure The Value Of X Is
News Leon
Mar 28, 2025 · 5 min read
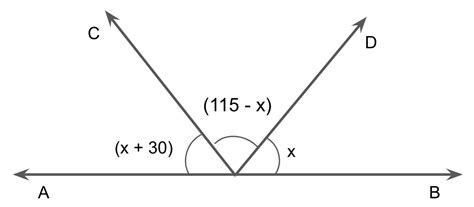
Table of Contents
Decoding the Mystery: Unveiling the Value of 'x' in Geometric Figures
Finding the value of 'x' in geometric figures is a fundamental skill in mathematics, crucial for problem-solving and a gateway to more advanced concepts. This comprehensive guide delves into various methods and strategies to determine the value of 'x', covering a range of geometric shapes and principles. While we can't analyze a specific figure without seeing it, we'll explore common scenarios and techniques, enabling you to tackle similar problems effectively. This article is designed to be both informative and practically applicable, serving as your go-to resource for solving geometric equations.
Keywords: find x, value of x, geometry problems, geometric equations, solving for x, geometric principles, angles, triangles, quadrilaterals, circles, problem-solving strategies, mathematics, algebra, geometry solutions
Understanding the Fundamentals: Key Geometric Principles
Before diving into specific problem types, let's review some crucial geometric principles that form the foundation of solving for 'x':
-
Angles: The sum of angles in a triangle always equals 180°. In a quadrilateral, the sum is 360°. Understanding supplementary (adding up to 180°) and complementary (adding up to 90°) angles is vital. Vertical angles are equal.
-
Triangles: Different types of triangles—equilateral (all sides and angles equal), isosceles (two equal sides and angles), right-angled (one 90° angle)—have unique properties that help solve for unknowns. The Pythagorean theorem (a² + b² = c²) applies to right-angled triangles, relating the lengths of the sides.
-
Quadrilaterals: Squares, rectangles, parallelograms, rhombuses, and trapezoids all have specific properties regarding angles, side lengths, and diagonals. Knowing these properties is crucial for establishing equations to solve for 'x'.
-
Circles: Understanding the relationship between radii, diameters, chords, tangents, and angles within circles is essential. The circumference and area formulas are frequently used in solving problems involving circles.
-
Similar Figures: Figures that have the same shape but different sizes are similar. Corresponding angles in similar figures are equal, and the ratios of corresponding sides are constant. This proportionality is key to finding unknown values.
-
Congruent Figures: Figures that have the same shape and size are congruent. All corresponding angles and sides are equal.
Common Methods for Solving for 'x'
The method used to solve for 'x' depends heavily on the type of geometric figure and the information provided. Here are some common approaches:
1. Utilizing Angle Relationships:
-
Triangles: If you know two angles in a triangle, you can easily find the third angle using the fact that their sum is 180°. For example, if two angles are 50° and 70°, then x (the third angle) = 180° - 50° - 70° = 60°.
-
Quadrilaterals: Similarly, if you know three angles in a quadrilateral, you can find the fourth angle (x) because the sum of angles is 360°.
-
Supplementary and Complementary Angles: Look for pairs of angles that form supplementary or complementary angles. This will provide equations that can be solved for 'x'.
2. Applying the Pythagorean Theorem:
This theorem is exclusively used for right-angled triangles. If you know two sides, you can find the third using the formula a² + b² = c², where 'c' is the hypotenuse (the side opposite the right angle).
3. Using Properties of Specific Geometric Shapes:
-
Isosceles Triangles: Remember that two sides and their opposite angles are equal. This can create equations to solve for 'x'.
-
Squares and Rectangles: All angles are 90°, and opposite sides are equal.
-
Parallelograms: Opposite sides and angles are equal.
-
Rhombuses: All sides are equal, and opposite angles are equal.
-
Trapezoids: At least one pair of opposite sides is parallel.
4. Utilizing Similar Figures:
If two figures are similar, the ratios of corresponding sides are equal. Set up a proportion to solve for 'x'. For instance, if the ratio of corresponding sides is 2:3, and one side in the larger figure is 12, then the corresponding side in the smaller figure (x) can be found by solving the proportion: 2/3 = x/12.
5. Solving Equations:
Often, the process of finding 'x' involves setting up and solving algebraic equations. This can involve:
-
Linear Equations: Simple equations involving 'x' with a power of 1.
-
Quadratic Equations: Equations where 'x' is raised to the power of 2. These often require factoring or using the quadratic formula.
Advanced Techniques and Problem-Solving Strategies
Tackling complex geometric problems often requires a combination of the techniques described above and strategic thinking:
-
Breaking Down Complex Figures: Divide complex figures into simpler shapes (triangles, quadrilaterals) to simplify the problem. This allows you to solve for individual parts before combining the results.
-
Visualizing and Drawing Diagrams: A clear, accurate diagram is crucial. Draw additional lines or construct auxiliary figures to reveal hidden relationships and create solvable equations.
-
Systematic Approach: Follow a systematic approach. Identify known information, determine the unknown (x), and choose the most appropriate method to find its value.
-
Checking your work: Always check your answer. Does it make sense in the context of the figure?
Example Scenarios and Solutions
While we cannot provide a solution to a figure not presented, let’s illustrate how to find 'x' in different scenarios:
Scenario 1: Finding 'x' in a Triangle:
Let's assume a triangle has angles of 40° and 70°. To find the third angle, x:
180° = 40° + 70° + x x = 180° - 40° - 70° x = 70°
Scenario 2: Finding 'x' in a Right-Angled Triangle using Pythagoras:
Consider a right-angled triangle with one leg of length 3 and hypotenuse of length 5. We need to find the length of the other leg (x):
a² + b² = c² 3² + x² = 5² 9 + x² = 25 x² = 16 x = 4
Scenario 3: Finding 'x' in Similar Triangles:
Two similar triangles have corresponding sides in the ratio 2:3. If one side of the larger triangle is 12, the corresponding side of the smaller triangle (x) is:
2/3 = x/12 x = (2 * 12) / 3 x = 8
Conclusion: Mastering the Art of Finding 'x'
Finding the value of 'x' in geometric figures is a skill developed through practice and understanding of fundamental geometric principles. By mastering the techniques outlined in this guide—using angle relationships, applying the Pythagorean theorem, exploiting properties of different shapes, and leveraging similar figures—you'll be well-equipped to solve a wide range of geometric problems. Remember to always approach problems systematically, visualize accurately, and check your work. With consistent effort and practice, you will confidently unlock the secrets hidden within geometric figures and solve for 'x' in any situation.
Latest Posts
Latest Posts
-
One Fathom Is Equal To In Feet
Mar 31, 2025
-
The Sum Of 3 Consecutive Numbers Is 72
Mar 31, 2025
-
How Do You Write 1 00 As A Percentage
Mar 31, 2025
-
Draw The Bohr Model For Aluminum
Mar 31, 2025
-
Which Particles Are Transferred During A Redox Reaction
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about In The Following Figure The Value Of X Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
