If Qt Is Perpendicular To Pr
News Leon
Mar 30, 2025 · 6 min read
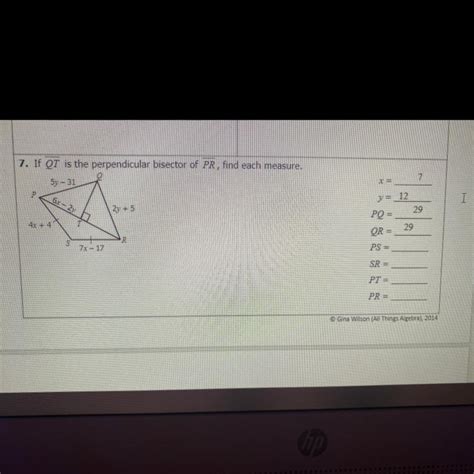
Table of Contents
If QT is Perpendicular to PR: Exploring Geometric Relationships
This article delves into the geometric implications when a line segment, QT, is perpendicular to another line segment, PR. We will explore various scenarios, theorems, and their applications, demonstrating how this seemingly simple relationship unlocks a wealth of geometrical properties and problem-solving techniques. Understanding this fundamental concept is crucial for mastering geometry at various levels, from high school to advanced mathematics.
Understanding Perpendicularity
Before diving into the specifics of QT being perpendicular to PR, let's establish a clear understanding of perpendicularity itself. Two lines or line segments are considered perpendicular if they intersect at a right angle (90 degrees). This relationship is denoted using the symbol ⊥, so we would write QT ⊥ PR to indicate that QT is perpendicular to PR. This simple statement carries significant weight in geometry because it leads to many important deductions and applications.
Key Properties of Perpendicular Lines
-
Right Angle Formation: The most fundamental property is the creation of a 90-degree angle at the point of intersection. This right angle is crucial in many geometrical proofs and constructions.
-
Distance Minimization: A perpendicular line segment from a point to a line represents the shortest distance between that point and the line. This property is extensively used in various applications, including finding the distance from a point to a line or plane.
-
Symmetry and Reflection: Perpendicular lines often exhibit symmetry. Reflecting a point or shape across a perpendicular line can reveal interesting relationships and properties.
Exploring Scenarios when QT ⊥ PR
The implications of QT ⊥ PR depend heavily on the context of the problem. We will examine a few scenarios to illustrate the diverse applications of this relationship:
Scenario 1: QT as an Altitude in a Triangle
Imagine a triangle PQR. If QT is a line segment originating from vertex Q and intersecting PR at a right angle (T), then QT is known as the altitude of the triangle from vertex Q. The altitude is the perpendicular distance from the vertex to the opposite side.
Implications:
-
Area Calculation: The area of triangle PQR can be calculated using the formula: Area = (1/2) * base * height, where the base is the length of PR and the height is the length of QT.
-
Orthocenter: The intersection point of the three altitudes of a triangle is called the orthocenter.
-
Right-Angled Triangles: The altitude divides the original triangle into two smaller right-angled triangles: PQT and RQT. This allows us to apply Pythagorean theorem and trigonometric functions.
Example: If PR = 10 and QT = 6, then the area of triangle PQR is (1/2) * 10 * 6 = 30 square units.
Scenario 2: QT as a Perpendicular Bisector
If QT is perpendicular to PR and T is the midpoint of PR, then QT is the perpendicular bisector of PR. This means QT divides PR into two equal segments (PT = TR) at a right angle.
Implications:
-
Equal Distances: Any point on QT is equidistant from points P and R. This property is fundamental in constructions involving circles and loci.
-
Symmetry: The line QT creates a line of symmetry; reflecting any point on one side of QT across the line will result in a corresponding point on the other side.
-
Circle Constructions: The perpendicular bisector is crucial in constructing the circumcenter of a triangle (the center of the circle passing through all three vertices).
Scenario 3: QT as a Line of Reflection
If QT is perpendicular to PR, then we can use it as a line of reflection. Reflecting a point or shape across QT will create a mirror image. The distance from the original point to QT will be equal to the distance from the reflected point to QT.
Implications:
-
Symmetry: This generates symmetrical shapes and patterns.
-
Geometric Transformations: This concept is essential in understanding geometric transformations such as reflections and rotations.
Scenario 4: QT in Coordinate Geometry
If the coordinates of points P, Q, R, and T are known, then we can use the properties of perpendicular lines in coordinate geometry. The slope of QT (m_QT) will be the negative reciprocal of the slope of PR (m_PR), meaning m_QT = -1/m_PR. This relationship allows us to determine if QT is perpendicular to PR using their slopes.
Implications:
-
Equation of Lines: We can find the equations of lines QT and PR and verify their perpendicularity using their slopes.
-
Distance Calculations: We can use the distance formula to calculate the lengths of QT and PR.
-
Point of Intersection: We can find the coordinates of T (the intersection point of QT and PR) using systems of equations.
Theorems and Applications
The perpendicularity of QT to PR often interacts with other important geometrical theorems, leading to further deductions and applications:
Pythagorean Theorem
If QT ⊥ PR in a right-angled triangle (e.g., Scenario 1), the Pythagorean theorem applies to triangles PQT and RQT. This theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Application: Calculating the length of unknown sides in right-angled triangles.
Trigonometric Functions
In right-angled triangles created by the perpendicular QT (Scenario 1), trigonometric functions like sine, cosine, and tangent can be applied to find the angles and side lengths.
Application: Solving problems involving angles and side lengths in right-angled triangles.
Similar Triangles
In certain scenarios, the perpendicular QT can create similar triangles. Similar triangles have the same angles but different sizes.
Application: Determining ratios of side lengths and solving problems involving proportions.
Problem Solving and Practical Applications
The concepts discussed above are not merely theoretical; they have numerous practical applications:
-
Engineering and Architecture: Perpendicularity is crucial in designing structures, ensuring stability and proper alignment.
-
Surveying and Mapping: Determining distances and angles using perpendicular lines is essential in surveying and mapping.
-
Computer Graphics: Perpendicularity plays a vital role in computer graphics, determining the orientation and position of objects.
-
Physics: Many physics problems, especially those involving forces and vectors, utilize the concept of perpendicularity.
Conclusion: The Significance of Perpendicularity
The relationship of QT being perpendicular to PR is a fundamental concept in geometry with far-reaching implications. Understanding this relationship allows us to solve a wide range of problems, from calculating areas of triangles to determining distances and angles. The ability to recognize and apply the properties of perpendicular lines is essential for anyone studying geometry or working in fields that rely heavily on spatial reasoning and geometric principles. This seemingly simple statement unlocks a complex world of geometrical possibilities, making it a cornerstone of geometric understanding and problem-solving. By mastering this fundamental concept, one can confidently approach more complex geometrical challenges and appreciate the elegance and power of geometric relationships.
Latest Posts
Latest Posts
-
All Real Numbers Are Rational Numbers True Or False
Apr 01, 2025
-
Which Of The Following Is A Function That Money Serves
Apr 01, 2025
-
The Most Abundant Compound In Most Living Things Is
Apr 01, 2025
-
How Can We Change The Polarity Of An Electromagnet
Apr 01, 2025
-
A Mother Beats Up Her Daughter Because She Was Drunk
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about If Qt Is Perpendicular To Pr . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
