If A Ball Is Thrown Vertically Upward
News Leon
Apr 05, 2025 · 6 min read
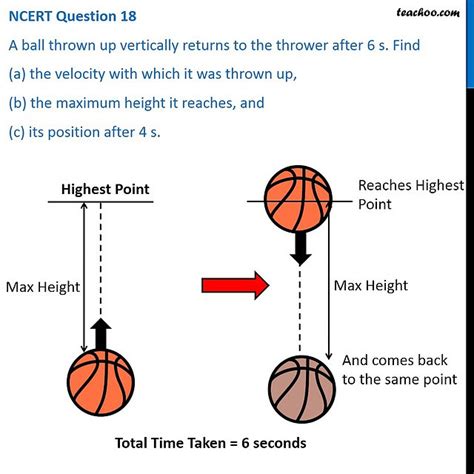
Table of Contents
If a Ball is Thrown Vertically Upward: A Deep Dive into Projectile Motion
Throwing a ball vertically upward seems simple, but it's a fascinating example of projectile motion, revealing fundamental principles of physics. This seemingly straightforward act encapsulates concepts like gravity, acceleration, velocity, and displacement, all interacting to dictate the ball's trajectory. Let's delve into the details, exploring the physics behind this common occurrence.
Understanding the Forces at Play
The primary force acting on the ball is gravity. Gravity constantly pulls the ball downwards towards the Earth's center, causing a downward acceleration of approximately 9.8 m/s² (this value, denoted as 'g', can vary slightly depending on location). This acceleration is constant throughout the ball's flight, regardless of its velocity. While the ball is moving upwards, gravity acts to decelerate it, eventually bringing it to a complete stop at its highest point. Once the ball starts its descent, gravity accelerates it downwards.
Air resistance, also known as drag, is another force that influences the ball's motion, though often neglected in simplified models. Air resistance opposes the ball's motion, meaning it acts upwards when the ball is going up and downwards when it's coming down. This force is dependent on several factors, including the ball's speed, size, shape, and the density of the air. In most introductory physics problems, air resistance is ignored to simplify calculations, providing a good approximation of the ball's motion. However, in real-world scenarios, air resistance significantly affects the ball's trajectory, especially over longer distances or with lighter, less aerodynamic objects.
Analyzing the Motion: Key Concepts
To fully understand the ball's vertical journey, we need to grasp the following key concepts:
1. Velocity: A Measure of Speed and Direction
Velocity is a vector quantity, meaning it possesses both magnitude (speed) and direction. As the ball travels upwards, its velocity is positive (assuming upwards is defined as the positive direction). Gravity continuously reduces this positive velocity until it reaches zero at the apex of its trajectory. As the ball descends, its velocity becomes negative, increasing in magnitude as gravity accelerates it downwards.
2. Acceleration: The Rate of Change of Velocity
Acceleration is the rate at which an object's velocity changes. In the case of the ball, the acceleration due to gravity is constant and directed downwards (-9.8 m/s²). This constant downward acceleration means the ball's velocity changes by 9.8 m/s every second.
3. Displacement: The Change in Position
Displacement is the vector quantity that measures the change in an object's position from its starting point. For the complete upward and downward journey, the displacement is zero if the ball lands at the same point from which it was thrown. The displacement during the upward leg is positive and the displacement during the downward leg is negative.
4. Time of Flight: The Duration of the Journey
The time of flight is the total time the ball spends in the air, from the moment it's thrown until it returns to the same height. This time is symmetric, meaning the time taken to reach the highest point is equal to the time taken to fall back down to the starting point, assuming no air resistance.
The Equations of Motion: Predicting the Ball's Trajectory
The kinematic equations of motion provide a mathematical framework for predicting the ball's position, velocity, and acceleration at any point in its flight. These equations, neglecting air resistance, are:
- v = u + at: Final velocity (v) equals initial velocity (u) plus acceleration (a) multiplied by time (t).
- s = ut + (1/2)at²: Displacement (s) equals initial velocity (u) multiplied by time (t) plus half of acceleration (a) multiplied by time squared (t²).
- v² = u² + 2as: Final velocity squared (v²) equals initial velocity squared (u²) plus two times acceleration (a) multiplied by displacement (s).
Where:
- u is the initial velocity (positive when thrown upwards).
- v is the final velocity.
- a is the acceleration due to gravity (-9.8 m/s²).
- s is the displacement.
- t is the time.
These equations can be used to determine various aspects of the ball's trajectory, such as:
- Maximum Height: The highest point the ball reaches. This occurs when the final velocity (v) becomes zero.
- Time to Reach Maximum Height: The time it takes for the ball to reach its highest point. This can be calculated using the first equation (v = u + at), setting v = 0.
- Total Time of Flight: The total time the ball remains in the air. This is twice the time it takes to reach the maximum height.
- Velocity at Any Point: The velocity of the ball at any given time during its flight.
The Influence of Air Resistance: A More Realistic Model
While the kinematic equations provide a simplified model, the real-world scenario involves air resistance. Air resistance is a complex force, dependent on several factors, making precise calculations challenging. However, we can qualitatively understand its effects:
- Reduced Maximum Height: Air resistance opposes the upward motion, reducing the ball's upward velocity and thus its maximum height.
- Shorter Time of Flight: The downward force of air resistance during the ascent and the upward force during the descent reduces the overall time the ball spends in the air.
- Asymmetrical Trajectory: The upward and downward portions of the trajectory become asymmetrical due to the varying effects of air resistance at different speeds. The descent is typically faster than the ascent.
- Terminal Velocity: As the ball falls, air resistance increases with velocity. Eventually, the upward force of air resistance equals the downward force of gravity, resulting in a constant velocity called terminal velocity.
Incorporating air resistance into calculations requires more advanced mathematical models, often involving differential equations. These models account for the complex relationship between air resistance, velocity, and other factors.
Applications and Real-World Examples
Understanding projectile motion, even in the simplified case of a vertically thrown ball, has numerous applications in various fields:
- Sports: Analyzing the trajectory of a ball in sports like basketball, baseball, or volleyball helps athletes improve their skills and optimize their techniques. Factors like launch angle, initial velocity, and air resistance all play crucial roles.
- Engineering: Understanding projectile motion is essential in designing and analyzing the trajectory of rockets, missiles, and other projectiles. Accurate predictions are critical for their safe and effective operation.
- Meteorology: Studying the motion of weather balloons and other atmospheric probes relies on understanding projectile motion, considering factors like wind speed and air density.
- Military Applications: Ballistics, the science of projectile motion, is fundamental in designing and deploying artillery and other weaponry.
Conclusion: A Simple Act, Complex Physics
Throwing a ball vertically upward, a seemingly mundane act, reveals the intricate interplay of fundamental physics principles. While simplified models neglecting air resistance offer a good starting point for understanding the basic concepts, a more realistic model must incorporate air resistance to accurately describe the ball's motion. The principles governing projectile motion extend far beyond the simple act of throwing a ball, finding applications in numerous scientific and engineering disciplines. The study of this seemingly simple motion offers a gateway to understanding complex physical phenomena and their applications in the real world. Further exploration into advanced concepts like drag coefficients, terminal velocity, and numerical methods for solving more complex trajectory problems will solidify your understanding of this fundamental aspect of physics.
Latest Posts
Latest Posts
-
What Is The Boiling Point In Kelvin
Apr 06, 2025
-
How Many Seconds In A Year In Scientific Notation
Apr 06, 2025
-
What Is 0 005 As A Percentage
Apr 06, 2025
-
What Serous Membrane Covers The Lungs
Apr 06, 2025
-
What Is The Equation For Fermentation
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about If A Ball Is Thrown Vertically Upward . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
