How To Remember Greater Than And Less Than
News Leon
Mar 30, 2025 · 5 min read
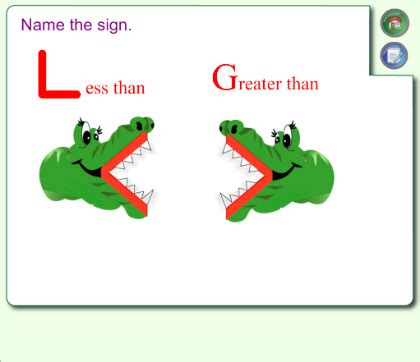
Table of Contents
How to Remember Greater Than and Less Than: A Comprehensive Guide
Remembering the difference between "greater than" (>) and "less than" (<) can be a surprisingly common stumbling block for students of all ages. This seemingly simple concept often trips up learners, hindering their progress in mathematics and related fields. This comprehensive guide provides a variety of techniques and strategies to help you, or your students, conquer this challenge once and for all. We will explore mnemonic devices, visual aids, real-world applications, and interactive exercises to solidify your understanding.
Understanding the Basics: The Alligator Analogy and Beyond
The most common mnemonic device for remembering greater than and less than is the "alligator analogy." The alligator's mouth always opens towards the larger number, as if it's trying to eat the bigger meal! This is a fantastic starting point, especially for younger learners.
However, relying solely on the alligator method might prove insufficient as mathematical concepts become more complex. Therefore, we'll delve into a variety of supplementary techniques to create a robust understanding.
Beyond the Alligator: Visualizing the Symbols
Look closely at the symbols themselves. Notice how the "greater than" symbol (>) resembles an arrow pointing to the right? You can think of it as a directional sign indicating the larger number. Conversely, the "less than" symbol (<) points to the left, signifying the smaller number. This visual association can be surprisingly effective.
Practice: Try visualizing these arrows in your mind when comparing numbers. Imagine the arrow pointing towards the larger value, reinforcing the symbol's meaning.
Number Line Representation: A Powerful Tool
A number line offers a powerful visual representation of numerical relationships. When comparing two numbers, plot them on the number line. The number appearing further to the right is always greater, and the number to the left is always less. This method transcends the limitations of simple number comparisons and easily extends to negative numbers and decimals.
Example: Compare -2 and 3. On a number line, 3 is to the right of -2, so 3 > -2 (3 is greater than -2).
The "Open Mouth" Technique: A Subtle Variation
Instead of focusing on the alligator, think of the symbol as an open mouth. The open side of the symbol always faces the larger number, like a mouth eagerly consuming the bigger amount. This provides a slight variation on the alligator analogy, catering to those who find the alligator image less intuitive.
Expanding Your Understanding: Tackling Complex Comparisons
While the alligator and number line methods are excellent starting points, they need to be supplemented with more sophisticated strategies as you progress to more advanced mathematical concepts.
Comparing Decimals and Fractions: A Systematic Approach
Comparing decimals and fractions can be challenging. However, by converting them to a common form (either both decimals or both fractions), comparison becomes significantly easier. Always ensure that the numbers are in the same format before applying the greater than or less than symbols.
Example: Compare 0.75 and ¾. Converting ¾ to a decimal (0.75), we see that they are equal.
Working with Negative Numbers: Mastering the Sign
Negative numbers often introduce confusion. Remember that the further a negative number is from zero, the smaller it is. For example, -5 is smaller than -2 because it is further to the left on the number line.
Example: Compare -10 and -5. Since -10 is further from zero than -5, -10 < -5 (-10 is less than -5).
Applying Your Knowledge: Real-World Scenarios
To solidify your understanding, apply your knowledge to real-world scenarios. This helps connect the abstract concept of greater than and less than to tangible experiences.
Example: Compare the prices of two items at the grocery store, the heights of two buildings, or the weights of two packages. These simple comparisons provide context and reinforce your understanding.
Interactive Exercises and Games: Engaging Your Mind
Active engagement is crucial for effective learning. Interactive exercises and games can make learning greater than and less than fun and memorable.
Create Your Own Comparison Scenarios
Challenge yourself by creating your own comparison problems. This active learning approach forces you to think critically and apply your knowledge in different contexts. Start with simple numbers and gradually increase the complexity.
Use Online Resources and Educational Games
Many websites and educational apps offer interactive games and quizzes focusing on greater than and less than. These games make learning enjoyable and provide instant feedback, accelerating the learning process. Search online for "greater than less than games" to find various options suitable for different age groups and skill levels.
Advanced Techniques for Long-Term Retention
To ensure long-term retention, incorporate these advanced techniques:
Spaced Repetition: The Power of Intervals
Spaced repetition is a powerful learning technique involving reviewing the material at increasing intervals. This method strengthens memory traces and enhances long-term retention. Review the concepts regularly, starting with frequent intervals and gradually spacing them out over time.
Teach Others: The Ultimate Test of Understanding
The best way to solidify your understanding of any concept is to teach it to someone else. Explaining the concepts of greater than and less than to a friend, family member, or even a stuffed animal will help identify any gaps in your own understanding and reinforce your knowledge.
Troubleshooting Common Errors and Misconceptions
Even with the best techniques, some common misconceptions might arise:
Confusing the Symbols: Address It Directly
If you find yourself constantly confusing the symbols, dedicate some time to consciously practice distinguishing between them. Use flashcards, write them repeatedly, and focus on associating the symbols with their correct meanings.
Difficulty with Negative Numbers: Return to Fundamentals
If negative numbers pose a particular challenge, revisit the basics. Utilize the number line and the concept of distance from zero to clarify the relationships between negative numbers.
Lack of Practice: Consistency is Key
The key to mastering any mathematical concept is consistent practice. Regularly review the material and engage in exercises to reinforce your understanding.
Conclusion: Mastering Greater Than and Less Than
Mastering the concepts of "greater than" and "less than" is fundamental to mathematical proficiency. By employing the various techniques outlined in this guide, from the simple alligator analogy to the more sophisticated spaced repetition method, you can confidently navigate numerical comparisons and build a strong foundation for future mathematical endeavors. Remember, consistent practice and active engagement are key to long-term retention and understanding. Embrace the challenge, and soon, you'll find comparing numbers as intuitive as breathing.
Latest Posts
Latest Posts
-
Genes On The Same Chromosome Are Said To Be
Apr 01, 2025
-
Which Of The Following Are Found In All Viruses
Apr 01, 2025
-
The Probability Of An Impossible Event Is
Apr 01, 2025
-
In What Way Are Energy And Nutrients Similar
Apr 01, 2025
-
Example Of Apology Letter For Lost Documents
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Remember Greater Than And Less Than . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
