How Many Lines Of Symmetry Does Scalene Triangle Have
News Leon
Mar 31, 2025 · 5 min read
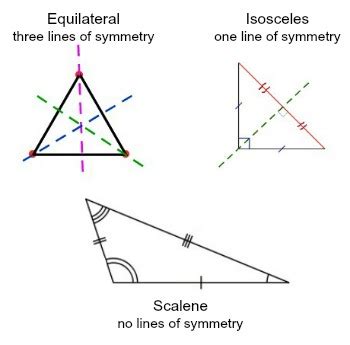
Table of Contents
How Many Lines of Symmetry Does a Scalene Triangle Have?
Understanding lines of symmetry is fundamental in geometry, and exploring this concept within different shapes reveals interesting mathematical properties. This article delves deep into the question: How many lines of symmetry does a scalene triangle have? We'll explore the definition of symmetry, different types of triangles, and ultimately answer the question definitively. We'll also touch on related concepts to provide a comprehensive understanding of this geometric topic.
Understanding Lines of Symmetry
A line of symmetry, also known as a line of reflectional symmetry, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, the two halves would perfectly overlap. Not all shapes possess lines of symmetry; some have many, while others have none. The number of lines of symmetry a shape has depends entirely on its properties and structure.
Identifying Lines of Symmetry
To identify lines of symmetry, consider the following:
- Visual Inspection: The simplest method is to visually assess the shape. Can you draw a line that divides the shape into two mirror-image halves?
- Folding Test: Imagine folding the shape. If the two halves perfectly align, the fold line represents a line of symmetry.
- Formal Geometric Methods: For more complex shapes, formal geometric methods and calculations might be necessary to determine the presence and number of lines of symmetry.
Types of Triangles and Their Symmetry
Triangles are classified based on their side lengths and angles. This classification directly impacts the number of lines of symmetry each type possesses:
1. Equilateral Triangle
An equilateral triangle has three sides of equal length and three angles of 60 degrees each. It possesses three lines of symmetry, one from each vertex to the midpoint of the opposite side. These lines are also the altitudes, medians, and angle bisectors of the triangle.
2. Isosceles Triangle
An isosceles triangle has two sides of equal length and two angles of equal measure. It has one line of symmetry, which bisects the unequal side and the angle opposite to it. This line is also the altitude and median from the vertex angle to the base.
3. Scalene Triangle
A scalene triangle has three sides of different lengths and three angles of different measures. This is where the core question of this article lies. A scalene triangle has no lines of symmetry. Because all sides and angles are different, there's no line that can divide it into two identical mirror-image halves. No matter where you draw a line through a scalene triangle, the resulting halves will always be dissimilar.
Why a Scalene Triangle Has No Lines of Symmetry
The absence of lines of symmetry in a scalene triangle stems directly from its defining characteristic: the unequal lengths of its sides. Let's consider why a line drawn through any part of a scalene triangle cannot be a line of symmetry:
-
Through a Vertex: A line drawn from a vertex will not divide the triangle into two congruent halves. The distances from the vertex to the points where the line intersects the opposite sides will be different, resulting in unequal areas on either side of the line.
-
Through the Midpoint of a Side: A line drawn through the midpoint of a side will not create two mirror-image halves. The angles formed on either side of the line will differ, as will the lengths of the segments created on the opposite side.
-
Any Other Line: Any other line drawn through a scalene triangle will inevitably produce two irregular, non-congruent regions. This lack of congruence eliminates the possibility of the line being a line of symmetry.
Mathematical Proof of Zero Lines of Symmetry in a Scalene Triangle
While visual inspection is usually sufficient to determine the absence of lines of symmetry, a more rigorous mathematical proof is possible. Let's consider a scalene triangle with vertices A, B, and C, and side lengths a, b, and c (a ≠ b ≠ c). Assume, for the sake of contradiction, that a line of symmetry exists. This line must either:
-
Pass through a vertex: If the line passes through a vertex, it must bisect the opposite side. However, in a scalene triangle, the perpendicular bisector of a side does not necessarily pass through the opposite vertex. Therefore, the line cannot be a line of symmetry.
-
Not pass through a vertex: If the line does not pass through a vertex, it must divide the triangle into two congruent polygons. However, this is impossible in a scalene triangle because the sides and angles are unequal. The areas on either side of the line would be different, contradicting the definition of a line of symmetry.
Therefore, by contradiction, a scalene triangle cannot have any lines of symmetry.
Expanding the Understanding: Symmetry in Other Geometric Shapes
While we've focused on triangles, the concept of lines of symmetry extends to many other geometric shapes:
- Circles: A circle has infinitely many lines of symmetry; any diameter acts as a line of symmetry.
- Squares: A square has four lines of symmetry: two diagonals and two lines connecting the midpoints of opposite sides.
- Rectangles: A rectangle has two lines of symmetry: lines connecting the midpoints of opposite sides.
- Regular Polygons: A regular polygon with n sides has n lines of symmetry.
Applications of Symmetry in Real-World Scenarios
Understanding symmetry is not just an abstract mathematical concept; it has practical applications in various fields:
- Art and Design: Symmetry is frequently used in art and design to create visually appealing and balanced compositions.
- Architecture: Symmetrical designs are common in architecture, contributing to the stability and aesthetic appeal of buildings.
- Nature: Symmetry is prevalent in nature, from the symmetrical wings of butterflies to the patterns in snowflakes.
- Engineering: Symmetry plays a crucial role in engineering design, ensuring stability and efficiency in structures and machines.
Conclusion
In summary, a scalene triangle has zero lines of symmetry. This is a direct consequence of its defining characteristic: the unequal lengths of its three sides. Understanding this property, along with the lines of symmetry in other shapes, provides a deeper understanding of geometric principles and their applications in various fields. This analysis highlights the importance of carefully considering the properties of a geometric shape when determining its lines of symmetry. The absence of symmetry in a scalene triangle reinforces the mathematical rigor underlying geometric classifications.
Latest Posts
Latest Posts
-
All Of The Following Characteristics Are Associated With Epithelium Except
Apr 02, 2025
-
This Organelle Pumps Out Excess Water
Apr 02, 2025
-
If The Demand For A Good Is Elastic Then
Apr 02, 2025
-
Solid Liquid Or Gas That A Wave Travels Through
Apr 02, 2025
-
What Is The Antiderivative Of E 2x
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does Scalene Triangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
