Solid Liquid Or Gas That A Wave Travels Through
News Leon
Apr 02, 2025 · 7 min read
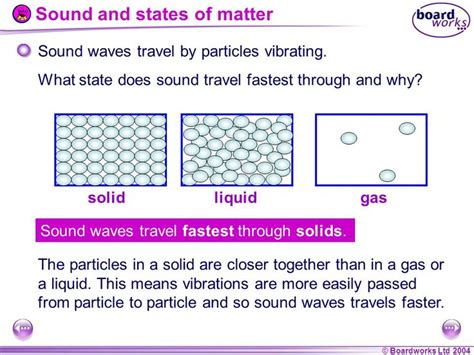
Table of Contents
The Medium Matters: Exploring How Waves Travel Through Solids, Liquids, and Gases
Waves are everywhere. From the gentle ripple in a pond to the seismic tremors shaking the earth, waves are a fundamental aspect of the physical world. But what exactly is a wave? And more importantly, what role does the medium – the solid, liquid, or gas through which a wave travels – play in its behavior? This comprehensive guide delves deep into the fascinating interplay between wave propagation and the properties of the material it passes through.
Understanding Wave Fundamentals
Before we dive into the specifics of different media, let's establish a basic understanding of wave characteristics. Waves are disturbances that transfer energy from one point to another without the permanent displacement of the medium itself. Think of a Mexican wave in a stadium – the people move up and down, transferring the wave's energy, but they don't permanently change their location.
There are two primary types of waves:
-
Mechanical Waves: These waves require a medium to propagate. Sound waves, seismic waves, and water waves are all examples of mechanical waves. The properties of the medium directly influence the speed, amplitude, and wavelength of these waves.
-
Electromagnetic Waves: These waves do not require a medium; they can travel through a vacuum. Light, radio waves, and X-rays are all electromagnetic waves. While their behavior is influenced by the medium they do pass through, they don't rely on a medium for their existence.
This article focuses on mechanical waves, specifically how they behave in solids, liquids, and gases.
Wave Propagation in Solids
Solids are characterized by their strong intermolecular forces and highly ordered structure. This structured arrangement significantly impacts how waves travel through them. The particles in a solid are tightly packed, leading to efficient energy transfer. As a result, mechanical waves generally travel faster in solids than in liquids or gases.
Types of Waves in Solids:
Solids can support two main types of mechanical waves:
-
Longitudinal Waves: In longitudinal waves, the particle displacement is parallel to the direction of wave propagation. Think of a slinky being pushed and pulled – the coils move back and forth along the same axis as the wave travels. Sound waves are a prime example of longitudinal waves. In solids, these waves are often referred to as compressional waves.
-
Transverse Waves: In transverse waves, the particle displacement is perpendicular to the direction of wave propagation. Imagine shaking a rope up and down – the wave travels along the rope, but the rope itself moves up and down. Seismic S-waves are examples of transverse waves. These waves require a medium with shear strength, something fluids lack.
The speed of these waves in solids depends on several factors, including:
-
Young's Modulus (Y): This measures a material's stiffness or resistance to deformation. A higher Young's modulus results in faster wave propagation.
-
Density (ρ): A denser material generally slows down wave propagation.
-
Poisson's Ratio (ν): This parameter reflects the relationship between lateral and axial strain. It influences the wave speed, particularly for transverse waves.
The specific formula for wave speed (v) varies depending on the type of wave:
-
Longitudinal waves:
v = √(Y(1-ν)/ρ(1+ν)(1-2ν))(This equation is an approximation and can be more complex in certain scenarios). -
Transverse waves:
v = √(G/ρ)where G is the shear modulus.
Examples of Wave Propagation in Solids:
-
Sound Transmission: Solids are excellent conductors of sound. This is why you can hear sounds more clearly when your ear is pressed against a solid surface.
-
Seismic Waves: Earthquakes generate both longitudinal (P-waves) and transverse (S-waves) waves that travel through the Earth's solid layers. The difference in their speeds helps seismologists locate earthquake epicenters.
-
Ultrasound Imaging: Medical ultrasound uses high-frequency sound waves that propagate through soft tissues (solids) to create images of internal organs.
Wave Propagation in Liquids
Liquids have weaker intermolecular forces than solids, leading to greater particle mobility. This results in slower wave propagation compared to solids. Liquids primarily support longitudinal waves, as their lack of significant shear strength prevents the propagation of transverse waves.
The speed of sound in liquids depends on several factors, including:
-
Bulk Modulus (K): This measures a liquid's resistance to compression. A higher bulk modulus implies faster wave propagation.
-
Density (ρ): As with solids, higher density generally slows down wave propagation.
The formula for the speed of sound (v) in a liquid is:
v = √(K/ρ)
Examples of Wave Propagation in Liquids:
-
Underwater Sound: Sound travels considerably faster in water than in air. This is why sonar systems are used for underwater navigation and detection.
-
Ocean Waves: While ocean waves are more complex and involve surface tension and gravity, the underlying principle involves the propagation of longitudinal waves through the water.
-
Medical Ultrasound: Ultrasound imaging also uses the propagation of sound waves through liquids, such as amniotic fluid during pregnancy.
Wave Propagation in Gases
Gases have the weakest intermolecular forces and the most disordered structure of the three states of matter. Particles in a gas are widely spaced, resulting in less efficient energy transfer, and consequently, the slowest wave propagation speed. Similar to liquids, gases primarily support longitudinal waves.
The speed of sound in gases depends on:
-
Adiabatic Bulk Modulus (γP): The adiabatic bulk modulus accounts for the fact that sound waves propagate so quickly that the compression and expansion processes are essentially adiabatic (no heat exchange). γ represents the adiabatic index (ratio of specific heats), and P is the pressure.
-
Density (ρ): Again, higher density leads to slower wave speeds.
The formula for the speed of sound (v) in an ideal gas is:
v = √(γP/ρ)
This can also be expressed as:
v = √(γRT/M) where R is the ideal gas constant, T is the temperature, and M is the molar mass of the gas.
Examples of Wave Propagation in Gases:
-
Sound in Air: The most familiar example of wave propagation in a gas is the sound we hear every day. The speed of sound in air is affected by temperature and humidity.
-
Atmospheric Phenomena: Sound waves are involved in various atmospheric phenomena, such as thunder and the propagation of shock waves from explosions.
Comparing Wave Propagation Across Media
The table below summarizes the key differences in wave propagation through solids, liquids, and gases:
| Property | Solid | Liquid | Gas |
|---|---|---|---|
| Intermolecular Forces | Strong | Moderate | Weak |
| Particle Arrangement | Highly Ordered | Less Ordered | Disordered |
| Wave Speed | Fastest | Intermediate | Slowest |
| Longitudinal Waves | Supported | Supported | Supported |
| Transverse Waves | Supported | Not Generally Supported | Not Generally Supported |
| Examples | Sound, Seismic Waves | Underwater Sound, Ocean Waves | Sound in Air, Thunder |
Factors Affecting Wave Speed and Attenuation
Several factors influence the speed and attenuation (reduction in amplitude) of waves as they travel through a medium:
-
Temperature: Higher temperatures generally increase the speed of sound in all three states of matter. The increased kinetic energy of particles allows for faster energy transfer.
-
Pressure: The effect of pressure on wave speed depends on the medium. In gases, increasing pressure generally increases the speed of sound. In liquids and solids, the effect is more complex and depends on the material's compressibility.
-
Density: Higher density typically leads to slower wave speeds in all three states of matter.
-
Viscosity (Liquids and Gases): Viscosity, a measure of a fluid's resistance to flow, contributes to wave attenuation. Higher viscosity leads to greater energy dissipation and reduced wave amplitude.
-
Elasticity (Solids): The elastic properties of a solid, specifically its Young's modulus and shear modulus, are crucial in determining wave speed.
-
Humidity (Gases): In the case of air, humidity can slightly increase the speed of sound due to the lower density of humid air.
Conclusion: The Medium's Crucial Role
The medium through which a wave travels plays a critical role in determining its properties. The strong intermolecular forces and ordered structure of solids lead to fast wave propagation, supporting both longitudinal and transverse waves. Liquids, with weaker forces and less ordered structure, support longitudinal waves at intermediate speeds. Gases, with weak forces and disordered structure, have the slowest wave speeds, supporting primarily longitudinal waves. Understanding these relationships is fundamental to various fields, from seismology and acoustics to medical imaging and atmospheric science. Further research continues to explore the nuances of wave propagation in various media, leading to advancements in technology and our understanding of the physical world.
Latest Posts
Latest Posts
-
Which Subshell Is Represented By The Actinides Series
Apr 03, 2025
-
Find The Area Of Scalene Triangle
Apr 03, 2025
-
Which Of The Following Is True Of Muscle Contraction
Apr 03, 2025
-
Elements That Are Liquids At Room Temperature
Apr 03, 2025
-
Direction Of Propagation Of Electromagnetic Waves
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Solid Liquid Or Gas That A Wave Travels Through . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
