How Many Lines Of Symmetry Does A Scalene Triangle Have
News Leon
Apr 06, 2025 · 5 min read
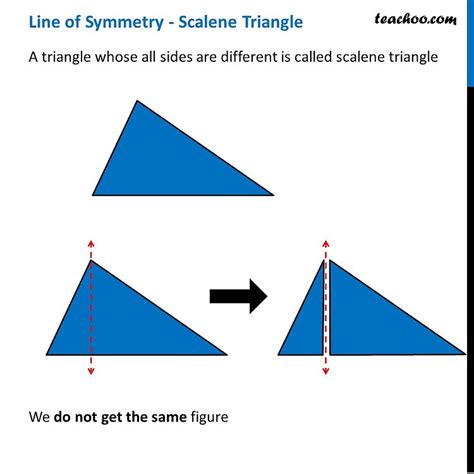
Table of Contents
How Many Lines of Symmetry Does a Scalene Triangle Have? Understanding Symmetry in Geometry
Symmetry, a fundamental concept in mathematics and geometry, refers to a balanced and proportionate arrangement of parts. Understanding lines of symmetry is crucial for grasping the properties of various shapes. This article delves into the concept of lines of symmetry, focusing specifically on scalene triangles and their lack thereof. We'll explore the definition of a scalene triangle, the concept of lines of symmetry in general, and why a scalene triangle, unlike many other shapes, possesses zero lines of symmetry. We will also briefly touch upon other types of triangles and their symmetry properties for comparison.
Defining a Scalene Triangle
Before we explore the lines of symmetry (or lack thereof), let's precisely define a scalene triangle. A scalene triangle is a polygon with three sides, where all three sides have different lengths. This inherent inequality in side lengths is the key characteristic that distinguishes a scalene triangle from other types of triangles such as isosceles and equilateral triangles.
Distinguishing Scalene Triangles from Other Triangles
To fully understand the unique properties of a scalene triangle, it's helpful to compare it to other types of triangles:
-
Isosceles Triangle: An isosceles triangle has at least two sides of equal length. This equality leads to certain symmetry properties, which we'll discuss later.
-
Equilateral Triangle: An equilateral triangle is a special case where all three sides are equal in length. This results in a high degree of symmetry.
-
Right-angled Triangle: A right-angled triangle has one angle measuring 90 degrees. While a right-angled triangle can be scalene, isosceles, or even, rarely, equilateral, the presence of a right angle doesn't inherently define its symmetry.
What is a Line of Symmetry?
A line of symmetry, also known as a line of reflection, divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, the two halves would perfectly overlap. This concept of mirroring is fundamental to understanding symmetry. Not all shapes possess lines of symmetry; some have none, while others have multiple.
Identifying Lines of Symmetry
Identifying lines of symmetry involves visually or mathematically checking whether folding a shape along a particular line results in perfect overlap. This can be done through observation, geometric construction, or algebraic methods, depending on the complexity of the shape.
The Absence of Lines of Symmetry in a Scalene Triangle
The crucial point is that a scalene triangle has zero lines of symmetry. This is a direct consequence of its defining characteristic: the inequality of its three sides. Because no two sides are equal, there is no line that can be drawn to divide the triangle into two mirror-image halves.
Visualizing the Lack of Symmetry
Imagine trying to fold a scalene triangle in half. No matter how you try to fold it, the two halves will never perfectly overlap. The unequal side lengths prevent any such perfect mirroring. This visual demonstration underscores the absence of lines of symmetry.
Mathematical Proof of Zero Lines of Symmetry
The lack of lines of symmetry in a scalene triangle can also be proven mathematically. A line of symmetry necessitates the existence of at least two equal angles or two equal sides. Since a scalene triangle, by definition, has no equal sides, it cannot possess a line of symmetry. Similarly, due to the relationship between side lengths and angles in a triangle, unequal sides lead to unequal angles. This absence of equal angles further reinforces the absence of any lines of symmetry.
Exploring Symmetry in Other Geometric Shapes
It is instructive to contrast the lack of symmetry in a scalene triangle with the symmetry found in other shapes.
Equilateral Triangle: Maximum Symmetry
An equilateral triangle, possessing three equal sides and three equal angles (60 degrees each), has three lines of symmetry. Each line passes through a vertex and the midpoint of the opposite side.
Isosceles Triangle: One Line of Symmetry
An isosceles triangle, with two equal sides and two equal angles, has one line of symmetry. This line bisects the angle formed by the two equal sides and also bisects the third side.
Other Shapes and their Lines of Symmetry
Many other geometric shapes possess lines of symmetry. For example:
- Square: Four lines of symmetry (two diagonals and two lines connecting midpoints of opposite sides).
- Rectangle: Two lines of symmetry (lines connecting midpoints of opposite sides).
- Circle: Infinite lines of symmetry (any diameter acts as a line of symmetry).
- Regular Polygon: A regular polygon with n sides has n lines of symmetry.
Applications of Symmetry in Real Life
Understanding lines of symmetry isn't just an abstract mathematical concept. It has numerous practical applications in various fields:
-
Art and Design: Artists and designers utilize symmetry to create visually appealing and balanced compositions. Symmetrical designs are often seen in architecture, logos, and artwork.
-
Nature: Symmetry is prevalent in nature, appearing in snowflakes, flowers, and many living organisms.
-
Engineering: Symmetry plays a critical role in engineering design, ensuring stability and balance in structures.
-
Science: Symmetry concepts are fundamental to various branches of science, including physics and chemistry.
Conclusion: The Unique Asymmetry of the Scalene Triangle
The scalene triangle, with its unique characteristic of having three unequal sides, stands out for its lack of symmetry. Unlike equilateral and isosceles triangles, which exhibit one or more lines of symmetry, the scalene triangle possesses none. This absence of symmetry is a direct consequence of its defining property and serves as a key distinguishing feature within the broader classification of triangles. Understanding this fundamental difference is essential for a thorough comprehension of geometric shapes and their properties. The lack of symmetry in a scalene triangle highlights the diversity and richness of geometric forms and their inherent properties. By exploring the concept of symmetry and its absence in different shapes, we gain a deeper appreciation for the beauty and elegance of geometry.
Latest Posts
Latest Posts
-
What Is Not True About Antibodies
Apr 07, 2025
-
Which Of The Following Is Not A Jovian Planet
Apr 07, 2025
-
Which Of The Following Statements About Variation Is False
Apr 07, 2025
-
What Direction Is The Template Strand Read
Apr 07, 2025
-
An Auditor Assesses The Risk Of Material Misstatement Because It
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does A Scalene Triangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
