How Many Lines Of Symmetry Circle
News Leon
Mar 31, 2025 · 6 min read
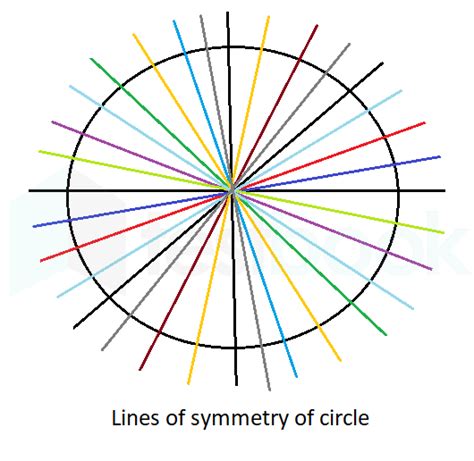
Table of Contents
How Many Lines of Symmetry Does a Circle Have? An Exploration of Rotational and Reflectional Symmetry
The seemingly simple question, "How many lines of symmetry does a circle have?" opens a fascinating exploration into the world of geometry, symmetry, and mathematical concepts. While the immediate answer might seem obvious, a deeper dive reveals a nuanced understanding of symmetry that extends beyond simple line reflections. This article will delve into the concept of lines of symmetry, specifically focusing on circles, and explore related concepts like rotational symmetry and the implications of infinite symmetry.
Understanding Lines of Symmetry
Before tackling the specific case of a circle, let's establish a firm understanding of what constitutes a line of symmetry. A line of symmetry, also known as a line of reflection, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along this line, the two halves would perfectly overlap. Think of a square: it has four lines of symmetry – two running vertically and horizontally through the center, and two running diagonally from corner to corner.
Types of Symmetry: Reflectional vs. Rotational
Symmetry isn't limited to just lines of reflection. Another crucial type is rotational symmetry. A shape possesses rotational symmetry if it can be rotated about a central point by less than 360 degrees and still look exactly the same. For example, a square has rotational symmetry of order 4 because it looks identical after rotations of 90, 180, and 270 degrees.
The Circle's Infinite Lines of Symmetry
Now, let's return to our central question: how many lines of symmetry does a circle have? The answer is infinite. This might seem counterintuitive at first, but consider the following:
-
Any diameter is a line of symmetry: A circle is perfectly symmetrical around its center. Any line passing through the center (a diameter) will divide the circle into two perfectly congruent semicircles. Since there are an infinite number of diameters in a circle, there are an infinite number of lines of symmetry. Imagine drawing a diameter; you can rotate that line by an infinitesimally small angle and still have another diameter – another line of symmetry.
-
Beyond Diameters: It's not just diameters. Any line passing through the center, regardless of its orientation, divides the circle into two mirror images. The concept of an infinite number of lines stems from the fact that you can draw a diameter at any angle, and every single one will be a line of symmetry.
Visualizing Infinite Lines of Symmetry
Imagine a circle drawn on a piece of paper. You can draw countless lines through the center point, each dividing the circle into two identical halves. The more lines you draw, the more evident it becomes that the number of potential lines of symmetry is limitless. This visual representation helps to grasp the concept of infinite lines of symmetry in a circle.
Rotational Symmetry of a Circle
In addition to its infinite lines of symmetry (reflectional symmetry), a circle also possesses rotational symmetry. A circle exhibits rotational symmetry of infinite order. This means that it can be rotated by any angle around its center, and it will always appear unchanged. This property is intrinsically linked to its infinite lines of symmetry; the rotational symmetry is a consequence of the reflectional symmetry.
The Mathematical Significance of Infinite Symmetry
The infinite symmetry of a circle is not just a geometric curiosity; it has significant mathematical implications. This property contributes to the circle's unique properties in various mathematical fields:
-
Calculus: The circle's symmetry simplifies many calculations in calculus, particularly those involving integration and differentiation. The symmetry allows for the use of simplifying techniques and reduces computational complexity.
-
Trigonometry: The circle is fundamental to trigonometry, and its symmetry plays a crucial role in defining trigonometric functions and identities. The symmetrical nature of the unit circle enables the derivation of many trigonometric relationships.
-
Geometry and Topology: The circle's infinite symmetry is a key concept in advanced geometry and topology, forming the basis of various theorems and proofs. Its symmetrical nature allows for the development of elegant mathematical models and representations.
Comparing Circle Symmetry to Other Shapes
It's instructive to compare the symmetry of a circle to that of other shapes:
-
Square: As mentioned earlier, a square has four lines of symmetry and rotational symmetry of order 4. It possesses a finite number of symmetry lines compared to a circle's infinite number.
-
Equilateral Triangle: An equilateral triangle has three lines of symmetry (each connecting a vertex to the midpoint of the opposite side) and rotational symmetry of order 3. Again, it has a finite number of symmetry elements.
-
Rectangle: A rectangle has two lines of symmetry and rotational symmetry of order 2 (180-degree rotation). Like the square and the triangle, its symmetry is finite.
The contrast between the finite symmetry of these shapes and the infinite symmetry of a circle highlights the circle's unique mathematical properties. This difference stems from the circle's fundamental definition as a set of points equidistant from a central point, a definition that intrinsically leads to infinite symmetry.
Applications of Circular Symmetry
The infinite symmetry of a circle is not merely a theoretical concept; it has numerous practical applications across various fields:
-
Engineering: Circular shapes are prevalent in engineering due to their inherent strength and symmetry. Wheels, gears, and pipes are just a few examples where circular symmetry is exploited for optimal functionality and structural integrity.
-
Architecture: Circular designs are often used in architecture for aesthetic and structural reasons. The symmetry of a circle can create visually appealing and balanced structures. The Pantheon in Rome is a prime example of circular architectural design.
-
Nature: Circular shapes are ubiquitous in nature, ranging from the sun and moon to the cross-sections of many plants and animals. This natural prevalence showcases the inherent efficiency and stability of circular symmetry.
-
Design: Circular motifs appear frequently in design, from logos and branding to artistic representations. The inherent balance and visual appeal of circular symmetry make it a popular choice for designers.
Conclusion: The Enduring Significance of Circular Symmetry
The question of how many lines of symmetry a circle possesses leads us down a path of exploration into the rich world of geometry and symmetry. The answer – infinite – is not simply a numerical fact but a fundamental property that underpins the circle's significance in mathematics, science, engineering, and design. The infinite lines of symmetry, coupled with its infinite rotational symmetry, contribute to the circle's unique and versatile nature, making it a fundamental shape with far-reaching implications across numerous disciplines. The enduring significance of circular symmetry lies not just in its mathematical elegance but also in its widespread practical applications and its captivating presence in both the natural and man-made worlds.
Latest Posts
Latest Posts
-
What Is The Aerial Part Of A Plant
Apr 01, 2025
-
A Semipermeable Membrane Is Placed Between
Apr 01, 2025
-
What Are The Two Body Forms Of Cnidarians
Apr 01, 2025
-
Eli The Ice Man Is Used To Remember
Apr 01, 2025
-
Density Of Water At 4 Degree Celsius
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
