Hollow Spherical Shell Moment Of Inertia
News Leon
Apr 05, 2025 · 5 min read
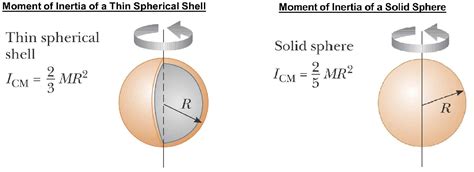
Table of Contents
Hollow Spherical Shell Moment of Inertia: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, describes an object's resistance to changes in its rotation. Understanding the moment of inertia is fundamental to analyzing rotational motion, calculating angular momentum, and predicting the behavior of rotating systems. This comprehensive guide delves into the intricacies of calculating the moment of inertia for a hollow spherical shell, exploring different approaches and providing practical applications.
Understanding Moment of Inertia
Before diving into the specifics of a hollow spherical shell, let's establish a solid understanding of the moment of inertia itself. It's a measure of how difficult it is to change the rotational speed of an object. Imagine trying to spin a bicycle wheel versus a solid disc of the same mass: the wheel, with its mass concentrated at the rim, will be significantly harder to accelerate or decelerate. This difference is quantified by the moment of inertia.
Mathematically, the moment of inertia (I) is defined as the sum of the products of each particle's mass (mᵢ) and the square of its distance (rᵢ²) from the axis of rotation:
I = Σ mᵢrᵢ²
For continuous mass distributions, like our hollow spherical shell, the summation becomes an integral:
I = ∫ r² dm
This integral requires careful consideration of the mass distribution and the chosen axis of rotation.
Deriving the Moment of Inertia for a Hollow Spherical Shell
The most common scenario involves calculating the moment of inertia of a hollow spherical shell about an axis passing through its center. This derivation requires integrating over the shell's surface. We'll break down the process step-by-step:
1. Defining the System
Consider a thin hollow spherical shell with a uniform mass density (ρ) and radius (R). The total mass (M) of the shell is related to its density and radius by:
M = 4πR²ρΔR
where ΔR represents the small thickness of the shell. In the limit of a truly thin shell, ΔR approaches zero.
2. Choosing a Coordinate System
We'll employ a spherical coordinate system (r, θ, φ), where 'r' is the radial distance from the center, 'θ' is the polar angle (measured from the z-axis), and 'φ' is the azimuthal angle (measured from the x-axis).
3. Expressing the Mass Element (dm)
The mass element dm can be expressed in terms of the surface area element dA and the surface mass density σ:
dm = σ dA
The surface area element in spherical coordinates is given by:
dA = R² sin θ dθ dφ
and the surface mass density σ is:
σ = M / (4πR²)
Substituting, we have:
dm = (M / 4πR²) R² sin θ dθ dφ = (M/4π) sin θ dθ dφ
4. Setting up the Integral
The moment of inertia about the z-axis (a common axis of rotation for a sphere) is given by:
I = ∫ r² dm = ∫ R² [(M/4π) sin θ dθ dφ]
Since 'r' is constant and equal to R for all points on the shell, we can simplify this to:
I = (MR²/4π) ∫∫ sin θ dθ dφ
5. Evaluating the Integral
The limits of integration for θ are from 0 to π, and for φ are from 0 to 2π. Therefore:
I = (MR²/4π) ∫₀²π ∫₀π sin θ dθ dφ = (MR²/4π) [2π] [-cos θ]₀π = (MR²/4π) (2π)(2) = (2/3)MR²
Therefore, the moment of inertia of a thin hollow spherical shell about an axis through its center is (2/3)MR².
Different Axes of Rotation
While the derivation above focuses on the moment of inertia about an axis passing through the center of the sphere, it's crucial to understand that the moment of inertia changes depending on the chosen axis. For a hollow spherical shell, the moment of inertia is the same for any axis passing through the center due to its inherent symmetry. However, if the axis of rotation is different, the calculation becomes more complex and will yield a different result.
Applications of Hollow Spherical Shell Moment of Inertia
The knowledge of the moment of inertia for a hollow spherical shell finds numerous applications in various fields:
- Astrophysics: Understanding the rotation of planets and celestial bodies, many of which can be approximated as hollow spherical shells. This is crucial for modeling their orbital dynamics and predicting their behavior in gravitational fields.
- Engineering: Designing rotating machinery, such as flywheels and gyroscopes. The moment of inertia directly impacts the rotational kinetic energy and angular momentum of these systems, influencing their performance and stability.
- Sports Science: Analyzing the motion of spherical objects in sports like bowling, golf, and baseball. The moment of inertia affects the ball's trajectory and spin, impacting its overall performance.
- Robotics: Designing robotic arms and manipulators. Understanding the moment of inertia of components is vital for accurate control and efficient movement of the robotic system.
Comparing with Solid Sphere
It's instructive to compare the moment of inertia of a hollow spherical shell with that of a solid sphere of the same mass and radius. The moment of inertia of a solid sphere is (2/5)MR². Notice the difference: the hollow sphere has a larger moment of inertia. This reflects the fact that the mass is distributed farther from the axis of rotation in the hollow sphere, making it more resistant to changes in its rotation.
Parallel Axis Theorem
The parallel axis theorem provides a convenient way to calculate the moment of inertia about an axis parallel to an axis through the center of mass. If I<sub>cm</sub> is the moment of inertia about an axis through the center of mass, and 'd' is the distance between the two parallel axes, then the moment of inertia (I) about the parallel axis is:
I = I<sub>cm</sub> + Md²
This theorem is useful when calculating the moment of inertia about an axis that doesn't pass through the center of the sphere.
Conclusion
The moment of inertia of a hollow spherical shell is a fundamental concept with widespread applications across various scientific and engineering disciplines. Understanding its derivation and its implications is essential for accurately modeling rotational motion and predicting the behavior of rotating systems. This comprehensive guide has explored the intricacies of calculating the moment of inertia, highlighting different approaches and providing a foundation for further exploration of rotational dynamics. The comparison with the solid sphere, the parallel axis theorem, and real-world applications solidify the significance of this crucial concept. By mastering this concept, you'll have a powerful tool for tackling a wide array of problems involving rotating bodies.
Latest Posts
Latest Posts
-
Activation Energy Of The Forward Reaction
Apr 05, 2025
-
Which Part Of The Scapula Articulates With The Clavicle
Apr 05, 2025
-
Which Part Of A Plant Makes Food
Apr 05, 2025
-
At What Temperature Do Celsius And Fahrenheit Scales Coincide
Apr 05, 2025
-
Can A Triangle Have More Than 1 Obtuse Angle
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Hollow Spherical Shell Moment Of Inertia . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
