Can A Triangle Have More Than 1 Obtuse Angle
News Leon
Apr 05, 2025 · 5 min read
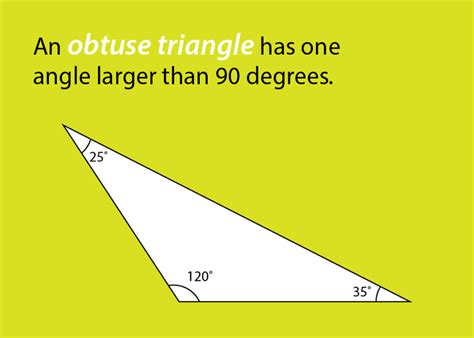
Table of Contents
Can a Triangle Have More Than 1 Obtuse Angle? A Deep Dive into Triangle Geometry
The question of whether a triangle can possess more than one obtuse angle is a fundamental concept in geometry. Understanding this requires a solid grasp of the definitions of different types of angles and the properties of triangles. This article will explore this question in detail, providing a comprehensive understanding of triangle geometry and the limitations imposed by the sum of angles in any triangle. We'll delve into the mathematical proof and provide clear, concise explanations to solidify your understanding.
Understanding Angles in Geometry
Before we tackle the main question, let's establish a firm foundation by defining the types of angles relevant to our discussion:
- Acute Angle: An angle measuring less than 90 degrees.
- Right Angle: An angle measuring exactly 90 degrees.
- Obtuse Angle: An angle measuring greater than 90 degrees and less than 180 degrees.
- Straight Angle: An angle measuring exactly 180 degrees.
The Sum of Angles in a Triangle: A Cornerstone of Geometry
One of the most fundamental theorems in geometry is that the sum of the interior angles of any triangle always equals 180 degrees. This holds true regardless of the triangle's shape or size – whether it's an equilateral triangle, an isosceles triangle, a scalene triangle, or any other variation. This theorem forms the bedrock of our investigation into the possibility of a triangle with multiple obtuse angles.
The Impossibility of Two Obtuse Angles in a Triangle: Mathematical Proof
Let's assume, for the sake of contradiction, that a triangle can have two obtuse angles. Let's denote these angles as A and B. Since both angles are obtuse, they must each measure greater than 90 degrees:
- A > 90°
- B > 90°
Now, let's consider the sum of these two angles:
- A + B > 90° + 90° = 180°
However, we know that the sum of all three angles in any triangle must equal 180 degrees. Let's denote the third angle as C. Therefore:
- A + B + C = 180°
Substituting our inequality (A + B > 180°) into this equation, we get:
- 180° + C > 180°
Subtracting 180° from both sides, we find:
- C > 0°
While this inequality is true (angle C must have some positive value), it doesn't lead to a contradiction directly. However, let's reconsider the original inequality: A + B > 180°. This implies that the sum of just two angles in our triangle already exceeds the total sum of angles allowed in any triangle (180°). This is a clear contradiction. There is no possible positive value for angle C that would satisfy both A + B + C = 180° and A + B > 180°.
Therefore, our initial assumption – that a triangle can have two obtuse angles – must be false. It is mathematically impossible for a triangle to possess more than one obtuse angle.
Visualizing the Impossibility
Imagine trying to construct a triangle with two obtuse angles. As you try to draw the sides, you'll find that the lines representing the two obtuse angles simply cannot connect to form a closed shape. They would diverge, preventing the formation of a triangle. This visual representation reinforces the mathematical proof.
Types of Triangles Based on Angles
Understanding the types of triangles classified by their angles further clarifies the impossibility of a triangle with more than one obtuse angle:
- Acute Triangle: All three angles are acute (less than 90°).
- Right Triangle: One angle is a right angle (90°), and the other two are acute.
- Obtuse Triangle: One angle is obtuse (greater than 90°), and the other two are acute.
Notice that in none of these classifications is it possible to have more than one obtuse angle.
Exploring Related Geometrical Concepts
While we've definitively answered the main question, let's explore some related geometrical concepts to enhance your understanding:
- Exterior Angles of a Triangle: Each exterior angle of a triangle is equal to the sum of the two opposite interior angles.
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Similar Triangles: Triangles that have the same shape but different sizes. Similar triangles have corresponding angles that are congruent.
Understanding these concepts provides a broader context for grasping the fundamental principles governing triangle geometry.
Practical Applications and Real-World Examples
The principles of triangle geometry, including the impossibility of multiple obtuse angles, have practical applications in various fields:
- Engineering: Structural design relies heavily on understanding the properties of triangles to ensure stability and strength. The rigidity of triangles makes them ideal for constructing stable frameworks.
- Architecture: From simple roof trusses to complex building designs, triangles play a crucial role in ensuring structural integrity.
- Surveying: Triangulation, a technique using triangles to measure distances and angles, is fundamental in surveying and mapping.
Conclusion: The Inviolable Rule of Triangle Angles
The impossibility of a triangle having more than one obtuse angle is a fundamental and inviolable rule in geometry. The mathematical proof, combined with visual intuition, clearly demonstrates that such a triangle cannot exist. This principle is crucial for understanding various aspects of geometry and has wide-ranging practical applications in various fields. By grasping this concept, you solidify your foundation in geometry and pave the way for further exploration of more advanced geometrical concepts. The sum of angles in a triangle always equals 180°, a cornerstone of geometry that dictates the types of triangles possible. Remember, only one obtuse angle can exist within a single triangle.
Latest Posts
Latest Posts
-
E How Many Electrons Are In Mg2
Apr 06, 2025
-
Spiders And Scorpions Belong To The Phylum
Apr 06, 2025
-
Distinguish Between A Chemical Reaction And A Chemical Equation
Apr 06, 2025
-
Which Of The Following Statements About Monsoons Are Correct
Apr 06, 2025
-
Provide An Acceptable Name For The Alkane Shown Below
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Can A Triangle Have More Than 1 Obtuse Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
