Geometric Mean Of 4 And 9
News Leon
Mar 30, 2025 · 6 min read
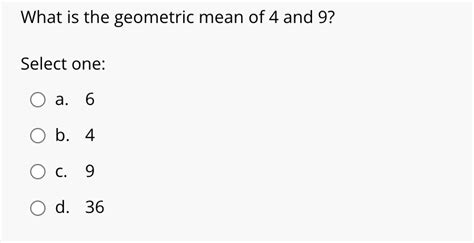
Table of Contents
Delving Deep into the Geometric Mean: A Comprehensive Exploration Using 4 and 9
The geometric mean, a concept often overshadowed by its more familiar arithmetic counterpart, plays a crucial role in various fields, from finance and statistics to geometry and music. Understanding its properties and applications is essential for anyone dealing with multiplicative relationships or proportional changes. This article will delve deep into the geometric mean, using the example of 4 and 9 to illustrate its calculation, properties, and practical applications. We'll explore its differences from the arithmetic mean, its relationship to other mathematical concepts, and its significance in real-world scenarios.
What is the Geometric Mean?
The geometric mean is a type of average that indicates the central tendency or typical value of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). For a set of 'n' non-negative numbers, the geometric mean is the nth root of the product of those numbers. For two numbers, like our example of 4 and 9, the calculation is straightforward:
Geometric Mean (GM) = √(a * b)
Where 'a' and 'b' are the two numbers. In our case:
GM(4, 9) = √(4 * 9) = √36 = 6
Therefore, the geometric mean of 4 and 9 is 6.
Arithmetic Mean vs. Geometric Mean: A Crucial Distinction
It's vital to understand the difference between the arithmetic mean (AM) and the geometric mean (GM). While the arithmetic mean sums the numbers and divides by the count, the geometric mean multiplies the numbers and takes the root. This fundamental difference leads to significant variations in the results, particularly when dealing with sets containing widely disparate values.
Let's compare the arithmetic and geometric means for 4 and 9:
- Arithmetic Mean (AM) = (4 + 9) / 2 = 6.5
- Geometric Mean (GM) = √(4 * 9) = 6
Notice the slight difference? This difference becomes more pronounced as the disparity between the numbers increases. The geometric mean is less sensitive to extreme values (outliers) than the arithmetic mean. This makes it a more robust measure of central tendency in certain contexts.
Properties of the Geometric Mean
The geometric mean possesses several important properties that contribute to its usefulness:
-
Always Less Than or Equal to the Arithmetic Mean: For any non-negative set of numbers, the geometric mean will always be less than or equal to the arithmetic mean. Equality holds only when all the numbers in the set are identical. This is known as the AM-GM inequality.
-
Invariance under Scaling: Multiplying all numbers in a set by a constant factor will multiply the geometric mean by the same factor. This property is highly useful in various applications, particularly in financial calculations involving rates of return.
-
Suitable for Multiplicative Relationships: The geometric mean is particularly well-suited for analyzing data where values are multiplied together, such as rates of growth or returns on investment. In such cases, it provides a more accurate representation of average change than the arithmetic mean.
Applications of the Geometric Mean
The geometric mean finds application in a wide range of fields:
1. Finance:
-
Average Rate of Return: When calculating the average annual rate of return on an investment over multiple periods, the geometric mean provides a more accurate measure than the arithmetic mean, accounting for the compounding effect of returns. Imagine an investment that doubles in one year and halves in the next. The arithmetic mean would suggest no change, but the geometric mean reflects the reality of no overall gain.
-
Portfolio Performance: In portfolio management, the geometric mean is used to calculate the average annual return of an investment portfolio, considering the compounding effect of returns across different assets.
2. Statistics:
-
Log-Normal Distributions: The geometric mean is naturally suited to datasets following a log-normal distribution, where the logarithm of the data follows a normal distribution. Such distributions frequently occur in various scientific and financial phenomena.
-
Index Numbers: In the construction of index numbers (like the Consumer Price Index or CPI), the geometric mean is often employed to avoid the potential bias introduced by using the arithmetic mean.
3. Geometry:
-
Similar Triangles: The geometric mean appears in geometrical relationships, for example, when finding the length of an altitude in a right-angled triangle. The altitude to the hypotenuse of a right triangle is the geometric mean of the segments it creates on the hypotenuse.
-
Mean Proportional: The geometric mean is sometimes called the mean proportional between two numbers. This concept is important in various geometric constructions.
4. Music:
- Frequency Ratios: In music theory, the geometric mean is used to calculate the frequency ratios between musical intervals. For example, the geometric mean of two frequencies determines the frequency that lies exactly halfway between them on a logarithmic scale, reflecting the perception of musical intervals.
5. Other Applications:
-
Image Processing: The geometric mean is used in image processing to calculate the average pixel value in an image, leading to more robust image representation than the arithmetic mean.
-
Engineering: The geometric mean plays a role in determining the effective values of alternating currents and voltages.
Deeper Dive: The AM-GM Inequality
The AM-GM inequality is a fundamental mathematical theorem stating that the arithmetic mean of a set of non-negative real numbers is always greater than or equal to the geometric mean of the same set. For two numbers, a and b, it can be expressed as:
(a + b) / 2 ≥ √(ab)
Equality holds only when a = b. The proof of this inequality can be demonstrated through various methods, including algebraic manipulation and using calculus. This inequality has profound implications in various mathematical proofs and problem-solving techniques. The AM-GM inequality provides a powerful tool for establishing bounds and inequalities in various mathematical contexts.
Let's apply this to our example of 4 and 9:
(4 + 9) / 2 = 6.5
√(4 * 9) = 6
As expected, the arithmetic mean (6.5) is greater than the geometric mean (6).
Conclusion: The Significance of the Geometric Mean
The geometric mean, although often less familiar than the arithmetic mean, is a powerful tool with widespread applications across diverse fields. Its insensitivity to outliers, suitability for multiplicative relationships, and elegant mathematical properties make it an indispensable concept for anyone working with data analysis, financial modeling, or various scientific and engineering applications. By understanding its calculation, properties, and applications, you can gain a deeper understanding of the underlying mathematical principles governing many real-world phenomena. The example of the geometric mean of 4 and 9 provides a simple yet fundamental illustration of its utility and significance in the world of mathematics and beyond. The exploration of the AM-GM inequality further underscores its importance in establishing mathematical relationships and solving problems. Remember to choose the appropriate average based on the nature of your data and the specific problem you are trying to solve. The geometric mean is a vital tool in your mathematical arsenal, providing valuable insights and accurate representations in situations where the arithmetic mean might fall short.
Latest Posts
Latest Posts
-
What Is The Atomic Number Of An Atom Equal To
Apr 01, 2025
-
Parathyroid Hormone Does All Of The Following Except
Apr 01, 2025
-
Which Structure Is Not Part Of A Neuron
Apr 01, 2025
-
An Asset Created By Prepayment Of An Insurance Premium Is
Apr 01, 2025
-
What Is The Study Of Snakes Called
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Geometric Mean Of 4 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
