Find The Value Of X In The Figure Below
News Leon
Mar 28, 2025 · 6 min read
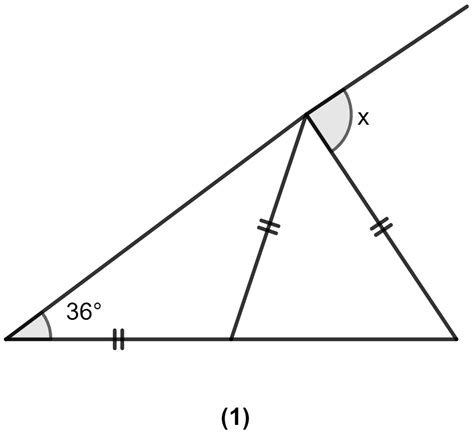
Table of Contents
Find the Value of x in the Figure Below: A Comprehensive Guide
Finding the value of 'x' in geometric figures is a fundamental skill in mathematics, particularly in geometry and trigonometry. This article will explore various methods and strategies for solving for 'x' in different geometric scenarios, ranging from simple equations to more complex problems involving angles, triangles, and other shapes. We will focus on developing a systematic approach to problem-solving, emphasizing understanding the underlying geometric principles rather than just memorizing formulas.
Understanding the Basics: Angles and Lines
Before diving into complex problems, let's review some essential geometric concepts that form the foundation for solving for 'x':
1. Angles:
- Acute Angle: An angle less than 90 degrees.
- Right Angle: An angle exactly equal to 90 degrees.
- Obtuse Angle: An angle greater than 90 degrees but less than 180 degrees.
- Straight Angle: An angle exactly equal to 180 degrees.
- Reflex Angle: An angle greater than 180 degrees but less than 360 degrees.
- Complementary Angles: Two angles whose sum is 90 degrees.
- Supplementary Angles: Two angles whose sum is 180 degrees.
- Vertically Opposite Angles: Angles opposite each other when two lines intersect. They are always equal.
2. Lines:
- Parallel Lines: Lines that never intersect, regardless of how far they are extended.
- Perpendicular Lines: Lines that intersect at a right angle (90 degrees).
- Transversal Line: A line that intersects two or more parallel lines.
Understanding these concepts is crucial for solving problems involving 'x' in geometric figures. Many problems will require applying these definitions and relationships to establish equations that can be solved to find the value of 'x'.
Solving for 'x' in Different Geometric Figures
Let's delve into various types of geometric problems where finding the value of 'x' is the objective. We'll explore different approaches and techniques for each scenario.
1. Triangles:
Triangles are fundamental shapes in geometry, and many problems involve finding the value of 'x' within their angles or sides.
a) The Angle Sum Property: The sum of the angles in any triangle is always 180 degrees. This is a powerful tool for finding unknown angles. If you know two angles of a triangle, you can easily find the third using this property. For example, if two angles are 60° and 70°, then x (the third angle) = 180° - 60° - 70° = 50°.
b) Isosceles Triangles: An isosceles triangle has two equal sides and two equal angles opposite those sides. Knowing this property can help determine the value of 'x' if you know one of the equal angles or sides.
c) Equilateral Triangles: An equilateral triangle has three equal sides and three equal angles, each measuring 60 degrees.
d) Similar Triangles: Similar triangles have the same shape but different sizes. Corresponding angles are equal, and the ratios of corresponding sides are constant. This proportionality can be used to set up equations and solve for 'x'.
2. Quadrilaterals:
Quadrilaterals are four-sided polygons. Different types of quadrilaterals have specific properties that can be used to find 'x'.
a) Rectangles and Squares: Rectangles have four right angles (90 degrees), and opposite sides are equal. Squares are a special type of rectangle with all four sides equal. These properties are useful in setting up equations to solve for 'x'.
b) Parallelograms: Parallelograms have opposite sides parallel and equal. Opposite angles are also equal. These properties provide relationships that can be used to find 'x'.
c) Trapezoids: Trapezoids have at least one pair of parallel sides. The angles between the parallel sides are supplementary (add up to 180 degrees).
d) Rhombuses: Rhombuses have all four sides equal, and opposite angles are equal.
3. Circles:
Circles involve angles and arcs, and finding 'x' often requires understanding the relationships between these elements.
a) Central Angles and Arcs: A central angle is an angle whose vertex is at the center of the circle. The measure of the central angle is equal to the measure of its intercepted arc.
b) Inscribed Angles: An inscribed angle is an angle whose vertex lies on the circle. The measure of an inscribed angle is half the measure of its intercepted arc.
c) Tangents and Secants: Tangents are lines that touch a circle at only one point. Secants are lines that intersect a circle at two points. There are specific relationships between the angles formed by tangents and secants and the arcs they intersect.
4. Advanced Techniques:
For more complex problems, you may need to employ more advanced techniques:
a) Trigonometry: Trigonometry utilizes trigonometric functions (sine, cosine, tangent) to relate angles and sides in triangles. This is particularly useful for solving problems involving right-angled triangles and oblique triangles.
b) Coordinate Geometry: Coordinate geometry uses coordinates to represent points and lines in a plane. This allows you to use algebraic equations to represent geometric relationships and solve for 'x'.
Example Problems and Solutions
Let's illustrate these concepts with some examples. Remember to always clearly define 'x' within the context of the problem.
Example 1: Finding 'x' in a Triangle
A triangle has angles of 50°, 70°, and x°. Find the value of x.
Solution: The sum of angles in a triangle is 180°. Therefore, 50° + 70° + x° = 180°. Solving for x, we get x = 180° - 50° - 70° = 60°.
Example 2: Finding 'x' in a Parallelogram
A parallelogram has adjacent angles of x° and (x + 40)°. Find the value of x.
Solution: Adjacent angles in a parallelogram are supplementary. Therefore, x + (x + 40) = 180. This simplifies to 2x + 40 = 180. Solving for x, we get 2x = 140, and x = 70°.
Example 3: Finding 'x' using Similar Triangles
Two similar triangles have corresponding sides of length 3 and 6, and 4 and x respectively. Find the value of x.
Solution: In similar triangles, the ratio of corresponding sides is constant. Therefore, 3/6 = 4/x. Cross-multiplying, we get 3x = 24, and x = 8.
Example 4: Finding 'x' using Trigonometry in a Right-Angled Triangle
A right-angled triangle has a hypotenuse of length 10 and an angle of 30°. The side opposite the 30° angle has length x. Find the value of x.
Solution: Using the trigonometric function sine, we have sin(30°) = x/10. Since sin(30°) = 0.5, we have 0.5 = x/10. Solving for x, we get x = 5.
Tips for Solving for 'x'
-
Draw a diagram: Always start by drawing a clear diagram of the figure. This helps visualize the relationships between angles and sides.
-
Identify the relevant geometric properties: Determine which geometric properties apply to the figure (e.g., angle sum property, properties of parallel lines, properties of specific shapes).
-
Write down equations: Translate the geometric relationships into algebraic equations involving 'x'.
-
Solve the equations: Use algebraic techniques to solve for the value of 'x'.
-
Check your answer: Always check if your solution is reasonable within the context of the problem.
By following these steps and practicing regularly, you will develop the skills and confidence to solve for 'x' in a wide variety of geometric figures. Remember that the key is to understand the underlying geometric principles and apply them systematically. This approach will not only help you find the correct answer but also deepen your understanding of geometry.
Latest Posts
Latest Posts
-
Do Gram Positive Bacteria Have Porins
Mar 31, 2025
-
Which Of The Following Compounds Is Most Soluble In Water
Mar 31, 2025
-
Part Of The Brain That Controls Breathing And Heartbeat
Mar 31, 2025
-
This Pair Of Structures Anchors The Spindle
Mar 31, 2025
-
Oxidation State Of Cl In Clo3
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Find The Value Of X In The Figure Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
