Find The Perimeter Of A Triangle With Vertices
News Leon
Apr 03, 2025 · 5 min read
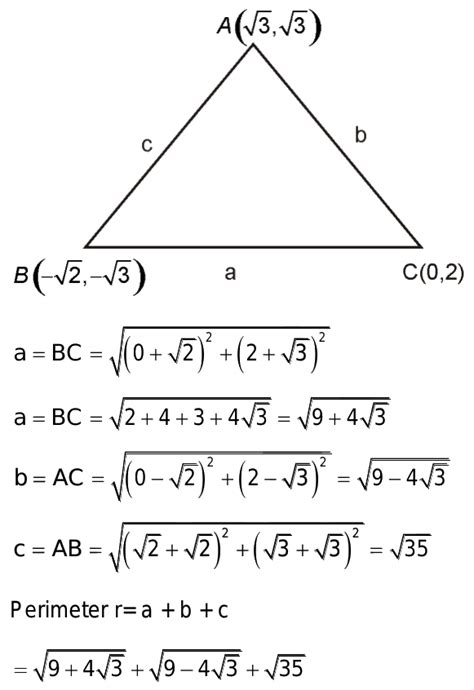
Table of Contents
Find the Perimeter of a Triangle with Vertices: A Comprehensive Guide
Finding the perimeter of a triangle given its vertices might seem like a straightforward task, but understanding the underlying principles and applying them effectively is crucial, especially when dealing with more complex scenarios. This comprehensive guide will delve into various methods, formulas, and practical examples to help you master this geometric concept. We'll cover everything from the basic distance formula to more advanced techniques, ensuring you can confidently calculate the perimeter of any triangle, no matter the complexity of its vertices.
Understanding the Fundamentals: Perimeter and Triangles
Before we jump into the calculations, let's establish a firm grasp of the fundamental concepts.
What is Perimeter?
The perimeter of any polygon, including a triangle, is the total distance around its exterior. Think of it as the length of a continuous path that traces the edges of the shape. For a triangle, this means summing the lengths of all three sides.
What are Vertices?
The vertices of a triangle (or any polygon) are the points where two or more sides meet. They define the shape and location of the triangle on a coordinate plane. We often represent vertices using coordinate pairs (x, y).
Method 1: Using the Distance Formula
The most common method for finding the perimeter of a triangle with given vertices is by using the distance formula. This formula calculates the distance between two points in a Cartesian coordinate system.
The Distance Formula
The distance d between two points (x₁, y₁) and (x₂, y₂) is given by:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Applying the Distance Formula to Triangles
Let's say we have a triangle with vertices A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃). To find the perimeter, we need to calculate the length of each side (AB, BC, and CA) using the distance formula and then sum them up.
- Length of AB: d₁ = √[(x₂ - x₁)² + (y₂ - y₁)²]
- Length of BC: d₂ = √[(x₃ - x₂)² + (y₃ - y₂)²]
- Length of CA: d₃ = √[(x₁ - x₃)² + (y₁ - y₃)²]
Perimeter = d₁ + d₂ + d₃
Example:
Let's find the perimeter of a triangle with vertices A(1, 2), B(4, 6), and C(7, 2).
- Length of AB: d₁ = √[(4 - 1)² + (6 - 2)²] = √(3² + 4²) = √25 = 5
- Length of BC: d₂ = √[(7 - 4)² + (2 - 6)²] = √(3² + (-4)²) = √25 = 5
- Length of CA: d₃ = √[(1 - 7)² + (2 - 2)²] = √((-6)² + 0²) = √36 = 6
Perimeter = 5 + 5 + 6 = 16
Therefore, the perimeter of the triangle is 16 units.
Method 2: Using the Pythagorean Theorem (for Right-Angled Triangles)
If you happen to know that the triangle is a right-angled triangle (meaning it has one 90-degree angle), you can use the Pythagorean theorem as a shortcut.
The Pythagorean Theorem
The Pythagorean theorem states that in a right-angled triangle with sides a, b, and hypotenuse c, the following relationship holds:
a² + b² = c²
Applying the Pythagorean Theorem
If you know the coordinates of the vertices and can identify the right angle, you can calculate the lengths of the two shorter sides (legs) using the distance formula (or by simply subtracting coordinates if the sides are parallel to the axes). Then, use the Pythagorean theorem to find the length of the hypotenuse. Finally, sum the lengths of all three sides to get the perimeter.
Example:
Consider a right-angled triangle with vertices A(0, 0), B(3, 0), and C(3, 4). The right angle is at B.
- Length of AB: AB = 3 (horizontal distance)
- Length of BC: BC = 4 (vertical distance)
- Length of AC (hypotenuse): AC² = AB² + BC² = 3² + 4² = 25; AC = 5
Perimeter = 3 + 4 + 5 = 12
Method 3: Using Heron's Formula (for Any Triangle)
Heron's formula provides a direct way to calculate the area of a triangle given the lengths of its three sides. While not directly calculating the perimeter, it's useful when you have the side lengths but not the coordinates. Once you find the side lengths using the distance formula, you can use Heron's formula to verify the area.
Heron's Formula
Given the side lengths a, b, and c, the semi-perimeter s is calculated as:
s = (a + b + c) / 2
Then, the area A is:
A = √[s(s - a)(s - b)(s - c)]
This formula is useful as a check for your perimeter calculations, particularly if you've used the distance formula to determine the side lengths.
Dealing with Complex Scenarios
The methods above handle most common cases. However, some situations might require additional steps or different approaches.
Triangles in Three-Dimensional Space
If your vertices are represented by three-dimensional coordinates (x, y, z), you'll need a slightly modified distance formula:
d = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
The rest of the process remains the same – calculate the length of each side using this modified formula and then sum them up to find the perimeter.
Using Vector Operations
For those familiar with vector algebra, calculating distances and perimeters can be done efficiently using vector operations. The length of a vector represents the distance between two points. The difference between two position vectors representing the vertices gives you the vector representing the side of the triangle. The magnitude of this vector is the length of the side. This method can be particularly helpful when dealing with larger sets of vertices or more complex geometric problems.
Practical Applications and Importance
Understanding how to find the perimeter of a triangle is crucial in many fields, including:
- Engineering: Calculating material needs for construction, design specifications, etc.
- Surveying: Determining land boundaries and areas.
- Computer Graphics: Creating and manipulating 3D models.
- Physics: Calculating the path of objects and their trajectories.
- Cartography: Measuring distances on maps and creating accurate representations.
Conclusion
Finding the perimeter of a triangle given its vertices is a fundamental geometric calculation with widespread applications. While the distance formula provides a reliable method for most situations, understanding alternative techniques like the Pythagorean theorem and Heron's formula expands your problem-solving capabilities. By mastering these methods and understanding their underlying principles, you'll be well-equipped to tackle various geometric problems and confidently navigate applications across numerous disciplines. Remember to always double-check your calculations and consider using alternative methods to verify your results. This approach not only improves accuracy but also deepens your understanding of the fundamental concepts involved.
Latest Posts
Latest Posts
-
Is Drawings A Debit Or Credit
Apr 04, 2025
-
Enzymes Are Catalysts That Increase The Rate Of Reactions By
Apr 04, 2025
-
Does Nitrogen Lose Or Gain Electrons
Apr 04, 2025
-
Able To Be Drawn Into Wire
Apr 04, 2025
-
A Food Chain Starts With A
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Perimeter Of A Triangle With Vertices . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
