Find The Measure Of Each Lettered Angle In The Figure
News Leon
Mar 30, 2025 · 7 min read
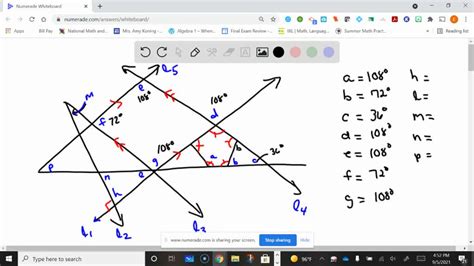
Table of Contents
Find the Measure of Each Lettered Angle in the Figure: A Comprehensive Guide
Finding the measure of angles within a geometric figure can seem daunting, but with a systematic approach and a solid understanding of geometric principles, it becomes a manageable and even enjoyable task. This comprehensive guide will walk you through various methods and strategies to solve for unknown angles, equipping you with the skills to tackle complex geometric problems with confidence. We'll cover a range of scenarios, from simple figures involving supplementary and complementary angles to more intricate diagrams involving triangles, parallel lines, and polygons.
Understanding Basic Angle Relationships
Before diving into complex figures, let's solidify our understanding of fundamental angle relationships. These relationships are the building blocks for solving more challenging problems.
1. Complementary Angles:
Complementary angles are two angles whose measures add up to 90 degrees. If you know the measure of one complementary angle, you can easily find the measure of the other by subtracting its value from 90 degrees.
Example: If angle A measures 35 degrees and is complementary to angle B, then angle B measures 90 - 35 = 55 degrees.
2. Supplementary Angles:
Supplementary angles are two angles whose measures add up to 180 degrees. Similar to complementary angles, knowing the measure of one supplementary angle allows you to calculate the measure of the other by subtracting its value from 180 degrees.
Example: If angle C measures 110 degrees and is supplementary to angle D, then angle D measures 180 - 110 = 70 degrees.
3. Vertical Angles:
Vertical angles are the angles opposite each other when two lines intersect. Vertical angles are always equal in measure.
Example: If angle E and angle F are vertical angles, and angle E measures 60 degrees, then angle F also measures 60 degrees.
4. Linear Pairs:
A linear pair consists of two adjacent angles that form a straight line. The sum of the measures of a linear pair is always 180 degrees. This is a direct consequence of supplementary angles.
Example: If angle G and angle H form a linear pair, and angle G measures 125 degrees, then angle H measures 180 - 125 = 55 degrees.
Solving for Angles in Triangles
Triangles form the foundation of many geometric problems. Understanding the angle relationships within triangles is crucial for solving for unknown angles.
1. The Sum of Angles in a Triangle:
The sum of the measures of the three interior angles of any triangle is always 180 degrees. This is a fundamental theorem in geometry.
Example: If a triangle has angles measuring x, y, and z degrees, then x + y + z = 180.
2. Isosceles Triangles:
An isosceles triangle has two sides of equal length. The angles opposite these equal sides are also equal in measure.
Example: If an isosceles triangle has two angles measuring 40 degrees each, then the third angle measures 180 - (40 + 40) = 100 degrees.
3. Equilateral Triangles:
An equilateral triangle has all three sides of equal length. All three angles in an equilateral triangle are equal and measure 60 degrees each.
Example: Each angle in an equilateral triangle measures 60 degrees.
Solving for Angles with Parallel Lines
Parallel lines intersected by a transversal line create a set of angles with specific relationships. Understanding these relationships is vital for solving many geometric problems.
1. Corresponding Angles:
Corresponding angles are angles that are in the same relative position at an intersection when a line intersects two other lines. If the two lines are parallel, corresponding angles are equal.
Example: If two parallel lines are intersected by a transversal, and a pair of corresponding angles measure 75 degrees, then the other corresponding angle also measures 75 degrees.
2. Alternate Interior Angles:
Alternate interior angles are angles that lie on opposite sides of the transversal and inside the two parallel lines. If the two lines are parallel, alternate interior angles are equal.
Example: If two parallel lines are intersected by a transversal, and a pair of alternate interior angles measure 110 degrees, then the other alternate interior angle also measures 110 degrees.
3. Alternate Exterior Angles:
Alternate exterior angles are angles that lie on opposite sides of the transversal and outside the two parallel lines. If the two lines are parallel, alternate exterior angles are equal.
Example: If two parallel lines are intersected by a transversal, and a pair of alternate exterior angles measure 80 degrees, then the other alternate exterior angle also measures 80 degrees.
4. Consecutive Interior Angles:
Consecutive interior angles are angles that lie on the same side of the transversal and inside the two parallel lines. If the two lines are parallel, consecutive interior angles are supplementary (their sum is 180 degrees).
Example: If two parallel lines are intersected by a transversal, and a pair of consecutive interior angles measure x and y degrees, then x + y = 180.
Solving for Angles in Polygons
Polygons are closed figures with three or more sides. The sum of the interior angles of a polygon can be calculated using a formula.
1. Sum of Interior Angles of a Polygon:
The sum of the interior angles of a polygon with n sides is given by the formula (n - 2) * 180 degrees.
Example: The sum of the interior angles of a pentagon (5 sides) is (5 - 2) * 180 = 540 degrees.
2. Regular Polygons:
A regular polygon has all sides and angles equal in measure. To find the measure of each interior angle of a regular polygon, divide the sum of the interior angles by the number of sides.
Example: Each interior angle of a regular hexagon (6 sides) measures [(6 - 2) * 180] / 6 = 120 degrees.
Solving Complex Geometric Problems: A Step-by-Step Approach
When faced with a complex figure containing multiple angles and shapes, follow these steps:
-
Identify known angles: Begin by noting down all the angles whose measures are already given in the figure.
-
Identify angle relationships: Look for complementary, supplementary, vertical, or linear pairs of angles. Identify triangles and parallel lines to utilize their respective angle relationships.
-
Use algebraic equations: Set up equations based on the angle relationships you've identified. Use variables to represent unknown angles.
-
Solve the equations: Solve the system of equations to find the values of the unknown angles.
-
Check your work: After calculating the values of the unknown angles, ensure that your solution satisfies all the known geometric principles and relationships.
Example Problem and Solution
Let's consider a figure with several unknown angles. We will use the principles discussed above to find their measures. (Insert a complex geometric figure here with lettered angles)
Solution:
-
Identify known angles: Assume we know the measure of angle A (e.g., A = 40°).
-
Identify angle relationships: Let's say angle A and angle B are supplementary. Angle C is a vertical angle to angle A. There might be a triangle involving angles B, C, and D.
-
Use algebraic equations: Since A and B are supplementary, A + B = 180°. Since A and C are vertical angles, A = C. The sum of angles in triangle BCD is B + C + D = 180°.
-
Solve the equations: Substitute the known value of A into the equations: 40° + B = 180°, so B = 140°. Since A = C, C = 40°. Finally, 140° + 40° + D = 180°, so D = 0°. Note: A result of 0° indicates there may be an error in the initial figure or assumptions made. We would need to re-evaluate the relationships.
-
Check your work: Verify your results against the original figure and ensure that all relationships hold true.
Remember to carefully analyze the figure, identify the relevant geometric principles, and use algebraic equations to solve for the unknown angles systematically. Practice is key to mastering this skill. The more problems you work through, the better you will become at recognizing patterns and applying the appropriate techniques.
Latest Posts
Latest Posts
-
Dense Irregular Connective Tissue Will Be Found In The
Apr 01, 2025
-
Which Of The Following Organisms Can Fix Nitrogen
Apr 01, 2025
-
Which Of The Following Is Correct About Viruses
Apr 01, 2025
-
How To Find Density Of Air
Apr 01, 2025
-
Which Of The Following Are Disaccharides
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Find The Measure Of Each Lettered Angle In The Figure . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
