Find The Energy Stored In The 20mh Inductor.
News Leon
Apr 03, 2025 · 5 min read
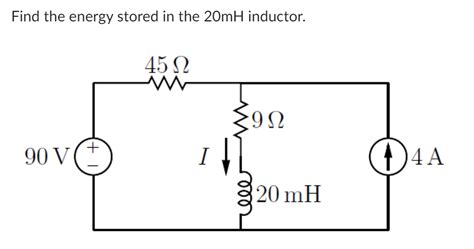
Table of Contents
- Find The Energy Stored In The 20mh Inductor.
- Table of Contents
- Finding the Energy Stored in a 20mH Inductor: A Comprehensive Guide
- Understanding Inductance and Energy Storage
- The Formula: The Heart of the Calculation
- Calculating Energy Stored in a 20mH Inductor: Step-by-Step Examples
- Scenario 1: Constant Current
- Scenario 2: Varying Current
- Scenario 3: Inductor in an RL Circuit
- Practical Implications and Real-World Applications
- Advanced Considerations: Non-Linear Inductors and Saturation
- Troubleshooting and Practical Tips
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Finding the Energy Stored in a 20mH Inductor: A Comprehensive Guide
Inductors, fundamental components in countless electrical circuits, store energy in a magnetic field. Understanding how to calculate this stored energy is crucial for circuit design, analysis, and troubleshooting. This comprehensive guide will delve into the intricacies of calculating the energy stored in a 20mH inductor, covering various scenarios and providing practical examples. We'll explore the fundamental principles, different approaches to calculation, and potential real-world applications.
Understanding Inductance and Energy Storage
An inductor, essentially a coil of wire, opposes changes in current. This opposition is quantified by its inductance (L), measured in Henries (H). When current flows through an inductor, it generates a magnetic field. The energy is stored within this magnetic field, not within the inductor itself. The higher the inductance and the larger the current, the greater the energy stored.
The Formula: The Heart of the Calculation
The energy (W) stored in an inductor is directly proportional to the square of the current (I) flowing through it and its inductance (L). This relationship is encapsulated in the following fundamental formula:
W = ½LI²
Where:
- W represents the energy stored in Joules (J)
- L represents the inductance in Henries (H)
- I represents the current in Amperes (A)
Calculating Energy Stored in a 20mH Inductor: Step-by-Step Examples
Let's apply this formula to various scenarios involving our 20mH inductor.
Scenario 1: Constant Current
Assume a constant current of 2 Amperes flows through the 20mH inductor. Let's calculate the energy stored:
-
Identify the known values: L = 20mH = 0.02H, I = 2A
-
Apply the formula: W = ½ * 0.02H * (2A)² = 0.04 Joules
Therefore, the energy stored in the 20mH inductor with a constant 2A current is 0.04 Joules.
Scenario 2: Varying Current
Real-world scenarios often involve currents that change over time. Let's consider a case where the current through the 20mH inductor varies according to a specific function. For instance, let's assume the current (I) is given by the function I(t) = 5sin(ωt) Amperes, where ω is the angular frequency.
To calculate the energy stored at a specific time, we substitute the current value at that time into the energy formula. For example, if we want to find the energy stored at time t = 0.1 seconds (assuming a suitable value for ω), we first calculate I(0.1) using the given function, and then plug that value into the energy formula:
-
Calculate I(t): Determine I(0.1) using the equation I(t) = 5sin(ωt). This requires knowing the value of ω (angular frequency). Let's assume ω = 10 rad/s for this example. Then, I(0.1) = 5sin(10 * 0.1) ≈ 4.55A.
-
Apply the formula: W = ½ * 0.02H * (4.55A)² ≈ 0.207 Joules.
Therefore, at t = 0.1 seconds, with the assumed angular frequency, the energy stored is approximately 0.207 Joules. Remember that this energy will continuously change as the current varies according to the sine function.
Scenario 3: Inductor in an RL Circuit
Consider a simple RL circuit with a resistor (R) and our 20mH inductor (L) connected in series with a DC voltage source. The current in this circuit doesn't instantaneously reach its maximum value; instead, it builds up over time. The current at any time t is given by:
I(t) = V/R * (1 - e^(-Rt/L))
Where:
- V is the source voltage
- R is the resistance
- t is the time
- e is the base of the natural logarithm (approximately 2.718)
To calculate the energy stored at a particular time, you would first determine the current using this equation and then substitute that current into the energy formula (W = ½LI²).
Practical Implications and Real-World Applications
Understanding energy storage in inductors is vital in numerous applications:
-
Energy Storage Systems: While not as efficient as capacitors for some applications, inductors play a role in energy storage systems, particularly in scenarios involving pulsed power or energy harvesting.
-
Switching Power Supplies: In switching power supplies, inductors are crucial for storing and releasing energy during the switching cycle, enabling efficient voltage conversion.
-
Filters: Inductors are used in filter circuits to smooth out variations in current or voltage. The energy stored helps maintain a relatively constant output.
-
Transformers: Transformers utilize the principle of energy storage and transfer in inductors to step up or step down voltage levels.
-
Wireless Charging: Inductive charging systems rely on the principle of energy transfer via magnetic fields generated by inductors.
Advanced Considerations: Non-Linear Inductors and Saturation
The formulas presented assume a linear inductor, where the inductance remains constant regardless of the current. However, real-world inductors exhibit non-linear behavior, especially at high currents. This is due to saturation of the core material. When the core saturates, the inductance decreases significantly, affecting the energy storage capacity. Accurate calculation in these scenarios requires considering the inductor's B-H curve and using more complex models.
Troubleshooting and Practical Tips
-
Accurate Measurement: Precise measurement of inductance and current is essential for accurate energy calculation. Using high-quality instruments is crucial.
-
Temperature Effects: The inductance of an inductor can vary with temperature. Consider temperature effects if operating conditions are extreme.
-
Core Losses: Real-world inductors experience energy losses due to core hysteresis and eddy currents. These losses reduce the actual energy stored compared to the theoretical value.
-
Simulation Software: Circuit simulation software can be invaluable for modeling circuits with inductors and verifying energy storage calculations under different conditions.
Conclusion
Calculating the energy stored in a 20mH inductor, or any inductor for that matter, is a fundamental skill for electrical engineers and anyone working with electrical circuits. While the basic formula is straightforward, understanding the context, including varying currents, non-linear behavior, and real-world effects, is essential for accurate analysis and design. This guide provides a comprehensive overview, equipping you with the knowledge and tools to confidently tackle various scenarios related to inductor energy storage. Remember that practical experience and the use of simulation tools significantly enhance your ability to analyze and design circuits involving inductors.
Latest Posts
Latest Posts
-
How Many Seconds In A Year In Scientific Notation
Apr 06, 2025
-
What Is 0 005 As A Percentage
Apr 06, 2025
-
What Serous Membrane Covers The Lungs
Apr 06, 2025
-
What Is The Equation For Fermentation
Apr 06, 2025
-
How Many Electrons Are In The Outer Shell Of Carbon
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Find The Energy Stored In The 20mh Inductor. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
