Find The Area Of The Parallelogram Shown
News Leon
Mar 30, 2025 · 5 min read
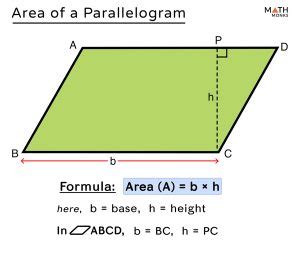
Table of Contents
- Find The Area Of The Parallelogram Shown
- Table of Contents
- Find the Area of a Parallelogram: A Comprehensive Guide
- Understanding the Parallelogram
- The Basic Formula: Base and Height
- Finding the Height: When it's not Directly Given
- Using Trigonometry
- Using Pythagorean Theorem
- Advanced Scenarios and Problem Solving
- Parallelograms within other shapes
- Using Coordinate Geometry
- Areas of Irregular Parallelograms
- Practical Applications and Real-World Examples
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Find the Area of a Parallelogram: A Comprehensive Guide
Finding the area of a parallelogram might seem like a simple task, especially after learning the basic formula. However, understanding the nuances of different approaches and applying them to various scenarios requires a deeper grasp of geometrical concepts. This comprehensive guide will delve into the intricacies of calculating the parallelogram's area, providing you with a robust understanding and equipping you with the skills to tackle diverse problem types.
Understanding the Parallelogram
Before diving into area calculations, let's solidify our understanding of parallelograms. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. This fundamental characteristic defines its geometric properties and underpins the various methods used to determine its area. Key features include:
- Opposite sides are parallel: This means lines extending from opposite sides will never intersect.
- Opposite sides are equal in length: The lengths of opposite sides are identical.
- Opposite angles are equal: The angles opposite each other have the same measure.
- Consecutive angles are supplementary: The sum of any two adjacent angles is 180 degrees.
The Basic Formula: Base and Height
The most fundamental method for calculating the area of a parallelogram involves its base and height. The formula is remarkably straightforward:
Area = base × height
- Base (b): This is the length of any one of the parallelogram's sides. You can choose any side as the base.
- Height (h): This is the perpendicular distance between the chosen base and its opposite side. It's crucial to understand that the height is always perpendicular (at a 90-degree angle) to the base. It's not simply the length of a side.
Example 1: Simple Calculation
Let's say we have a parallelogram with a base of 10 cm and a height of 5 cm. Applying the formula:
Area = 10 cm × 5 cm = 50 cm²
This calculation is straightforward when the height is explicitly provided. However, many problems require more nuanced approaches to determine the height.
Finding the Height: When it's not Directly Given
Often, the height isn't directly stated in a problem. In these cases, you might need to utilize trigonometry or other geometric principles to find it.
Using Trigonometry
If you know the length of one of the sides (other than the base) and the angle between that side and the base, you can use trigonometry to find the height. Specifically, you'll use the sine function:
height (h) = side length × sin(angle)
where:
- side length: The length of the side that forms the angle with the base.
- angle: The angle between the chosen side and the base.
Example 2: Using Trigonometry
Imagine a parallelogram with a base of 8 cm and a side length of 6 cm forming a 30-degree angle with the base. To find the height:
h = 6 cm × sin(30°) = 6 cm × 0.5 = 3 cm
Now, you can calculate the area:
Area = 8 cm × 3 cm = 24 cm²
Using Pythagorean Theorem
In some cases, the parallelogram might be embedded within a larger right-angled triangle, or you might be able to construct one using auxiliary lines. In such situations, the Pythagorean theorem (a² + b² = c²) can be invaluable for finding the height.
Example 3: Applying Pythagorean Theorem
Consider a parallelogram where the height is part of a right-angled triangle with a hypotenuse of 7 cm and one leg of 4 cm. Using the Pythagorean theorem:
h² + 4² = 7² h² + 16 = 49 h² = 33 h = √33 cm
You would then use this calculated height in the area formula.
Advanced Scenarios and Problem Solving
Let's tackle some more complex scenarios that require a deeper understanding of parallelogram properties and geometric reasoning:
Parallelograms within other shapes
Parallelograms can be embedded within more complex shapes. You might need to dissect the larger shape to isolate the parallelogram and then calculate its area using the methods described above. This often involves finding relevant lengths and angles through geometrical deductions.
Using Coordinate Geometry
When working with parallelograms defined by coordinates on a Cartesian plane, you can use vector calculations or determinant methods to compute the area. These methods involve finding the vectors representing the sides of the parallelogram and then using the cross product (or determinant) to calculate the area. This approach is especially useful when dealing with irregular or complex shapes.
Areas of Irregular Parallelograms
Irregular parallelograms, those that are not easily described with simple measurements, can be tackled by breaking them down into smaller, more manageable shapes (such as triangles or rectangles). By carefully calculating the areas of these smaller shapes and summing them, you can accurately determine the area of the irregular parallelogram.
Practical Applications and Real-World Examples
Understanding how to find the area of a parallelogram is not just an academic exercise; it has many practical applications:
- Engineering and Architecture: Calculating areas for flooring, roofing, and other construction materials.
- Agriculture: Estimating land area for crop planning and yield prediction.
- Graphic Design: Determining the area of shapes in layouts and designs.
- Physics: Calculations related to force and pressure in parallelogram-shaped structures.
Conclusion
Calculating the area of a parallelogram is a fundamental concept in geometry with wide-ranging applications. While the basic formula is simple, mastering the various methods for finding the height, particularly when it's not explicitly given, is crucial. By understanding the nuances of trigonometry, Pythagorean theorem, coordinate geometry, and problem-solving strategies, you'll be equipped to handle a broad spectrum of problems involving parallelograms, from simple calculations to complex scenarios involving irregular shapes and embedded parallelograms within larger geometrical figures. This comprehensive guide has provided you with the necessary tools and examples to confidently approach and solve such problems, allowing you to apply this knowledge in various practical applications. Remember to always carefully analyze the given information and choose the most appropriate method to solve the problem efficiently and accurately.
Latest Posts
Latest Posts
-
Which Of The Following Is A Primary Activity
Apr 02, 2025
-
Is Chlorine A Gas At Room Temperature
Apr 02, 2025
-
How Many Nanometers In A Micron
Apr 02, 2025
-
Which Proportionality Applies To Avogadros Law
Apr 02, 2025
-
Number Of Atoms In A Simple Cubic Unit Cell
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of The Parallelogram Shown . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
