Evaluate The Geometric Series Or State That It Diverges.
News Leon
Apr 02, 2025 · 5 min read
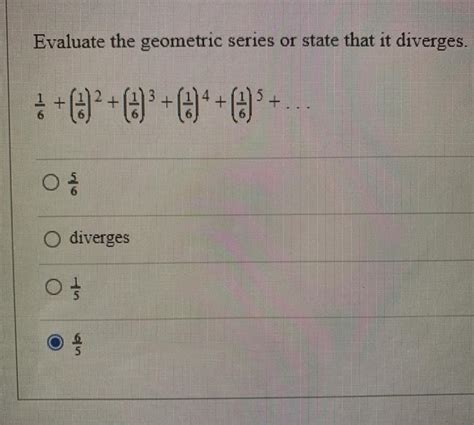
Table of Contents
Evaluate the Geometric Series or State That It Diverges
Geometric series are a fundamental concept in mathematics, particularly in calculus and analysis. Understanding how to evaluate them, or determine when they diverge, is crucial for many applications, from calculating compound interest to modeling physical phenomena. This comprehensive guide will walk you through the process of evaluating geometric series and identifying divergent ones. We'll explore the key formula, delve into examples showcasing different scenarios, and discuss the implications of convergence and divergence.
Understanding Geometric Series
A geometric series is a series where each term is obtained by multiplying the previous term by a constant value, called the common ratio (often denoted as 'r'). The general form of a geometric series is:
a + ar + ar² + ar³ + ...
Where:
- a is the first term of the series.
- r is the common ratio.
The series can be finite (ending after a specific number of terms) or infinite (continuing indefinitely). The behavior of the series – whether it converges to a finite sum or diverges to infinity – depends entirely on the value of the common ratio, r.
The Formula for the Sum of a Geometric Series
The sum of a finite geometric series with n terms is given by:
S<sub>n</sub> = a(1 - r<sup>n</sup>) / (1 - r) (where r ≠ 1)
If r = 1, then the sum is simply na (since each term is equal to a).
For an infinite geometric series, the formula for the sum is:
S<sub>∞</sub> = a / (1 - r) (where |r| < 1)
This formula only applies when the absolute value of the common ratio, |r|, is less than 1. If |r| ≥ 1, the infinite geometric series diverges; it doesn't approach a finite sum.
Determining Convergence and Divergence
The convergence or divergence of a geometric series hinges entirely on the value of the common ratio, 'r':
-
|r| < 1 (Convergence): If the absolute value of the common ratio is less than 1, the infinite geometric series converges to a finite sum. The terms get progressively smaller, approaching zero, and the sum approaches a limit.
-
|r| ≥ 1 (Divergence): If the absolute value of the common ratio is greater than or equal to 1, the infinite geometric series diverges. The terms either remain the same size or grow larger, preventing the series from approaching a finite sum. The sum will tend towards positive or negative infinity, or it will oscillate without approaching any limit.
Examples: Evaluating Geometric Series
Let's illustrate the evaluation process with various examples:
Example 1: Finite Geometric Series
Evaluate the sum of the first 5 terms of the geometric series: 2 + 6 + 18 + 54 + ...
Here, a = 2 and r = 3 (each term is multiplied by 3 to get the next). Using the formula for the sum of a finite geometric series:
S<sub>5</sub> = 2(1 - 3⁵) / (1 - 3) = 2(1 - 243) / (-2) = 2(-242) / (-2) = 242
The sum of the first 5 terms is 242.
Example 2: Infinite Geometric Series (Convergent)
Evaluate the sum of the infinite geometric series: 1 + ½ + ¼ + ⅛ + ...
Here, a = 1 and r = ½. Since |r| = ½ < 1, the series converges. Using the formula for the sum of an infinite geometric series:
S<sub>∞</sub> = 1 / (1 - ½) = 1 / (½) = 2
The sum of the infinite series is 2.
Example 3: Infinite Geometric Series (Divergent)
Determine whether the infinite geometric series 3 + 6 + 12 + 24 + ... converges or diverges.
Here, a = 3 and r = 2. Since |r| = 2 > 1, the series diverges. The terms grow increasingly larger, and the sum will approach infinity.
Example 4: Series with Negative Common Ratio (Convergent)
Evaluate the sum of the infinite geometric series: 1 - ½ + ¼ - ⅛ + ...
Here, a = 1 and r = -½. Since |r| = ½ < 1, the series converges. Using the formula:
S<sub>∞</sub> = 1 / (1 - (-½)) = 1 / (3/2) = 2/3
The sum of this alternating series is 2/3.
Example 5: Identifying a Geometric Series
Determine if the following series is geometric and if so, evaluate it: 4 + 12 + 36 + 108 +...
To determine if it's geometric, calculate the ratio between consecutive terms:
12/4 = 3 36/12 = 3 108/36 = 3
The ratio is constant (r=3). Since |r| > 1, the infinite series diverges. However, we can calculate the sum of a finite number of terms using the formula for a finite geometric series. For instance, the sum of the first 5 terms would be:
S<sub>5</sub> = 4(1 - 3⁵) / (1 - 3) = 4(1 - 243) / (-2) = 484
Applications of Geometric Series
Geometric series find numerous applications in diverse fields:
-
Finance: Calculating the future value of an investment with compound interest.
-
Physics: Modeling exponential decay, such as radioactive decay or the cooling of an object.
-
Computer Science: Analyzing algorithms and data structures.
-
Probability: Determining the probability of events in repeated trials.
Advanced Considerations: Dealing with Complexities
While the basic formula provides a straightforward approach, some series may require additional manipulation before applying the geometric series formula. For example:
-
Series that don't start at the first term (n=0 or n=1): You may need to factor out terms to transform the series into a standard form.
-
Telescoping series: These series have consecutive terms that cancel each other, often simplifying the sum calculation.
-
Series involving other functions: Geometric series principles can sometimes be applied to series involving trigonometric functions or other mathematical functions after some manipulation.
Conclusion
Geometric series are powerful tools for analyzing and evaluating sums. Understanding their behavior, particularly the critical role of the common ratio in determining convergence or divergence, is crucial for solving numerous problems in various fields. By mastering the formulas and techniques presented here, you'll be equipped to handle a wide range of geometric series problems, from simple evaluations to more complex scenarios requiring manipulation before application of the core principles. Remember to always carefully examine the common ratio to determine convergence or divergence before attempting to calculate the sum. Proper identification is the first, and often most crucial, step in successfully evaluating any geometric series.
Latest Posts
Latest Posts
-
1 Km 2 To M 2
Apr 03, 2025
-
Carbon Is Good Conductor Of Electricity
Apr 03, 2025
-
Figure Abcd Is A Kite Find The Value Of X
Apr 03, 2025
-
Distance North Or South Of The Equator Is Measured By
Apr 03, 2025
-
Which Subshell Is Represented By The Actinides Series
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Geometric Series Or State That It Diverges. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
