Figure Abcd Is A Kite Find The Value Of X
News Leon
Apr 03, 2025 · 6 min read
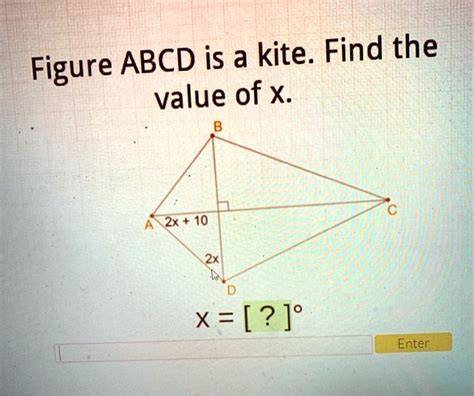
Table of Contents
Figure ABCD is a Kite: Finding the Value of x – A Comprehensive Guide
Finding the value of x in a kite problem might seem daunting at first, but with a systematic approach and a solid understanding of kite properties, it becomes surprisingly straightforward. This comprehensive guide will equip you with the knowledge and techniques to solve various problems involving kites and the unknown variable 'x'. We'll cover different scenarios, providing step-by-step solutions and helpful tips to boost your problem-solving skills.
Understanding the Properties of a Kite
Before diving into solving for 'x', let's refresh our understanding of kites. A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. This unique characteristic leads to several important properties:
-
Two pairs of adjacent congruent sides: This is the defining characteristic of a kite. Let's say in kite ABCD, AB = AD and BC = CD.
-
One pair of opposite angles are congruent: The angles between the non-congruent sides are equal. In our kite ABCD, ∠ABC = ∠ADC.
-
Diagonals are perpendicular: The diagonals of a kite intersect at a right angle (90 degrees).
-
One diagonal bisects the other: One diagonal is bisected by the other. This means it's cut into two equal segments. Typically, the diagonal connecting the vertices of the congruent sides bisects the other diagonal.
These properties form the bedrock of solving for 'x' in various kite problems. Let's explore different scenarios.
Scenario 1: Using Angle Properties to Find x
Problem: In kite ABCD, ∠ABC = 110° and ∠BCD = 80°. Find the value of x if ∠BAD = 2x + 10°.
Solution:
-
Identify the relevant property: We know that in a kite, opposite angles between unequal sides are equal. Therefore, ∠BAD = ∠BCD.
-
Set up the equation: We are given ∠BCD = 80° and ∠BAD = 2x + 10°. Since these angles are equal, we can set up the equation: 2x + 10 = 80.
-
Solve for x: Subtract 10 from both sides: 2x = 70. Divide both sides by 2: x = 35.
Therefore, the value of x is 35.
Scenario 2: Utilizing Side Lengths and the Pythagorean Theorem
Problem: In kite ABCD, AB = AD = 5 cm, and the diagonal AC has length 8 cm. If the length of BC is x + 2 cm, and AC is perpendicular to BD, find the value of x.
Solution:
-
Visualize the right-angled triangles: Since the diagonals are perpendicular, we can create two right-angled triangles: ΔABC and ΔADC. These triangles share the side AC.
-
Apply the Pythagorean Theorem: In right-angled triangle ΔABC, we have AB² = BC² + AC². Substituting the given values, we get: 5² = (x + 2)² + 4² (remember AC is bisected, so we take half the length).
-
Simplify and solve: This simplifies to 25 = (x + 2)² + 16. Subtracting 16 from both sides gives (x + 2)² = 9. Taking the square root of both sides results in x + 2 = ±3. Since length cannot be negative, x + 2 = 3, therefore x = 1.
Therefore, the value of x is 1 cm.
Scenario 3: Combining Angle and Side Properties
Problem: Kite ABCD has AB = AD = 6 cm and BC = CD = 8 cm. The diagonals intersect at point E. If AE = x + 2 and EC = 2x - 1, find the value of x.
Solution:
-
Recall the diagonal property: One diagonal of a kite bisects the other. In this case, AC bisects BD at point E.
-
Set up the equation: We are given AE = x + 2 and EC = 2x - 1. Since the diagonal AC bisects BD, AE = EC. Therefore, we can set up the equation: x + 2 = 2x - 1.
-
Solve for x: Subtracting x from both sides gives 2 = x - 1. Adding 1 to both sides yields x = 3.
Therefore, the value of x is 3 cm.
Scenario 4: Using Trigonometry in Kite Problems
Problem: In kite ABCD, AB = AD = 10 cm, and ∠BAD = 60°. The diagonal AC bisects ∠BAD. Find the value of x if the length of AC is x cm.
Solution:
-
Apply trigonometry to the triangle: Since AC bisects ∠BAD, we have two congruent right-angled triangles: ΔABC and ΔADC. In ΔABC, we have a 30-60-90 triangle.
-
Use trigonometric ratios: We can use the cosine ratio to find AC. In a 30-60-90 triangle, cos(30°) = adjacent/hypotenuse. Therefore, cos(30°) = AC/AB. Since cos(30°) = √3/2, we get (√3/2) = x/10.
-
Solve for x: Multiplying both sides by 10 gives x = 10√3/2 = 5√3.
Therefore, the value of x is 5√3 cm.
Scenario 5: Dealing with More Complex Kite Problems
Problem: Kite ABCD has AB = AD = 12 cm and BC = CD = 16 cm. The area of the kite is 192 cm². If the length of the shorter diagonal is 12 cm, find the length of the longer diagonal (x cm).
Solution:
-
Area of a kite formula: The area of a kite can be calculated using the formula: Area = (1/2) * d1 * d2, where d1 and d2 are the lengths of the diagonals.
-
Substitute known values: We are given the area (192 cm²) and the shorter diagonal (12 cm). Let x be the length of the longer diagonal. The formula becomes: 192 = (1/2) * 12 * x.
-
Solve for x: This simplifies to 192 = 6x. Dividing both sides by 6 gives x = 32.
Therefore, the value of x, the length of the longer diagonal, is 32 cm.
Advanced Tips and Considerations
-
Draw a diagram: Always start by drawing a clear diagram of the kite. This visual representation helps to understand the problem better and identify the relevant properties.
-
Label everything: Label all the given values and the unknown variable (x) on your diagram.
-
Break it down: Complex kite problems often involve multiple steps. Break the problem down into smaller, manageable parts.
-
Check your work: After you find the value of x, check your solution to ensure it makes sense within the context of the problem.
Conclusion: Mastering Kite Problems
Finding the value of x in a kite problem becomes manageable with a clear understanding of kite properties and a systematic approach to problem-solving. By applying the principles discussed in this guide—from using angle properties and Pythagorean theorem to employing trigonometric functions and the area formula—you can confidently tackle a wide range of kite problems. Remember to practice regularly, and you'll quickly develop the skills to solve even the most challenging scenarios. The key is breaking down complex problems into smaller, solvable parts and applying the relevant geometrical properties. With practice, you will master finding the value of 'x' in any kite configuration!
Latest Posts
Latest Posts
-
How To Find The Square Root Of Imperfect Squares
Apr 04, 2025
-
All Of The Following Are Money Market Instruments Except
Apr 04, 2025
-
Removes Nitrogen From The Atmosphere
Apr 04, 2025
-
Which Of The Following Is An Antibiotic
Apr 04, 2025
-
Which Of The Following Statements About Friction Is True
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Figure Abcd Is A Kite Find The Value Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
