Equation Of A Line Parallel To Y Axis
News Leon
Apr 05, 2025 · 5 min read
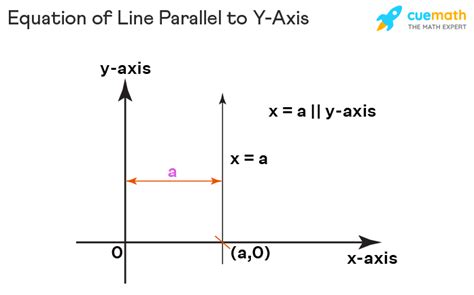
Table of Contents
The Equation of a Line Parallel to the Y-Axis: A Comprehensive Guide
The equation of a line parallel to the y-axis represents a fundamental concept in coordinate geometry. Understanding its derivation and applications is crucial for mastering various mathematical and graphical problems. This comprehensive guide delves into the equation of a line parallel to the y-axis, exploring its properties, derivations, and practical applications with numerous examples.
Understanding the Cartesian Coordinate System
Before we dive into the equation itself, let's refresh our understanding of the Cartesian coordinate system. This system uses two perpendicular lines, the x-axis (horizontal) and the y-axis (vertical), to define the location of any point in a plane using ordered pairs (x, y). The x-coordinate represents the horizontal distance from the origin (0, 0), and the y-coordinate represents the vertical distance from the origin.
Lines Parallel to the Y-Axis: A Visual Representation
Imagine a line perfectly vertical, never intersecting the x-axis. This line is parallel to the y-axis. Notice that every point on this vertical line shares the same x-coordinate. This observation forms the basis for deriving the equation.
Deriving the Equation: x = k
Consider a line parallel to the y-axis passing through a point (k, y), where 'k' is a constant and 'y' can take any value. Since the line is parallel to the y-axis, its x-coordinate remains constant regardless of the y-coordinate. Therefore, the equation of this line is simply:
x = k
where 'k' represents the x-intercept (the x-coordinate where the line intersects the x-axis). It's important to note that this line has no y-intercept, meaning it never intersects the y-axis unless k=0.
Exploring the Properties of x = k
-
Constant x-coordinate: The defining characteristic of a line parallel to the y-axis is that the x-coordinate of every point on the line is the same constant value, 'k'.
-
Undefined Slope: The slope of a vertical line is undefined. The slope is calculated as the change in y divided by the change in x (Δy/Δx). In this case, Δx is always zero, resulting in an undefined slope. This is because a vertical line has infinite slope - its steepness is so extreme that it's not definable using conventional slope terminology.
-
Infinite Number of Points: An infinite number of points satisfy the equation x = k, as the y-coordinate can take any real value.
-
No y-intercept: A line parallel to the y-axis, except for the line x=0, does not intersect the y-axis and hence has no y-intercept.
Examples and Applications
Let's explore some examples to solidify our understanding:
Example 1: Find the equation of the line parallel to the y-axis that passes through the point (3, 5).
Since the line is parallel to the y-axis, its equation will be of the form x = k. The x-coordinate of the given point is 3, so the equation of the line is:
x = 3
Example 2: Graph the line represented by the equation x = -2.
This equation represents a vertical line passing through the x-axis at x = -2. Every point on this line will have an x-coordinate of -2. You can plot points like (-2, 0), (-2, 1), (-2, -1), (-2, 10), etc., to visualize the line.
Example 3: Determine if the points (4, 2) and (4, 7) lie on the same line.
The x-coordinates of both points are the same (4). This implies that both points lie on a vertical line whose equation is x = 4. Therefore, they lie on the same vertical line parallel to the y-axis.
Example 4: Real-world application - Mapping
Consider a map where the x-axis represents the east-west direction and the y-axis represents the north-south direction. A line parallel to the y-axis could represent a street running perfectly north-south, where all points along the street have the same east-west coordinate (x = k).
Example 5: Finding the distance between parallel lines
Suppose you have two parallel lines, x = 2 and x = 7. The distance between these lines is simply the absolute difference between their x-intercepts: |7 - 2| = 5 units. This distance remains constant regardless of the y-coordinate.
Comparing with Lines Parallel to the X-Axis
It's important to distinguish between lines parallel to the y-axis (x = k) and lines parallel to the x-axis (y = k). Lines parallel to the x-axis have a slope of zero and represent horizontal lines. Their y-coordinate remains constant regardless of the x-coordinate.
Solving Problems Involving Lines Parallel to the Y-Axis
Many geometry problems involve lines parallel to the y-axis. These problems often require finding the equation of the line, determining if points lie on the line, calculating distances, and understanding the relationship between these lines and other geometrical figures.
For instance, problems might involve finding the intersection of a line parallel to the y-axis and another line with a defined slope. The solution would involve substituting the x-value from the equation of the vertical line into the equation of the other line to find the y-coordinate of the intersection point.
Advanced Applications: Calculus and Linear Algebra
The concept of lines parallel to the y-axis extends into more advanced mathematical fields. In calculus, understanding vertical asymptotes—which represent lines where a function approaches infinity or negative infinity—is crucial. Many vertical asymptotes are represented by equations of the form x = k. Similarly, in linear algebra, vertical lines are frequently encountered when analyzing systems of linear equations or performing matrix operations.
Conclusion: Mastering the Equation x = k
The equation x = k, representing a line parallel to the y-axis, is a fundamental concept in coordinate geometry with far-reaching implications. Understanding its derivation, properties, and applications is crucial for anyone studying mathematics or related fields. From simple graphing to complex calculus problems, mastering the equation x = k forms a solid foundation for more advanced mathematical concepts. Remember the key characteristics – constant x-coordinate, undefined slope, and no y-intercept (except for x=0) – to confidently tackle any problem involving lines parallel to the y-axis. Practice solving various problems, and you'll quickly master this essential aspect of coordinate geometry.
Latest Posts
Latest Posts
-
Differences Between Onion Epidermal And Human Epithelial Cells
Apr 05, 2025
-
Choose The True Statement About The Krebs Cycle
Apr 05, 2025
-
Five More Than The Quotient Of A Number And 4
Apr 05, 2025
-
Hollow Spherical Shell Moment Of Inertia
Apr 05, 2025
-
Which Of The Following Is True For Displacement
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Equation Of A Line Parallel To Y Axis . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
