Five More Than The Quotient Of A Number And 4
News Leon
Apr 05, 2025 · 5 min read
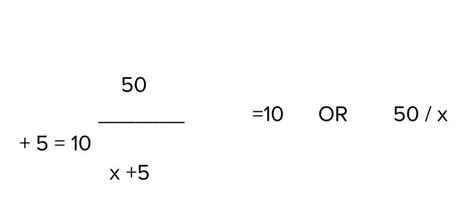
Table of Contents
Five More Than the Quotient of a Number and 4: A Deep Dive into Mathematical Expressions
This article explores the mathematical expression "five more than the quotient of a number and 4," dissecting its meaning, translating it into algebraic notation, solving related problems, and extending the concept to more complex scenarios. We'll cover various aspects, including:
Understanding the Expression
The phrase "five more than the quotient of a number and 4" is a verbal description of a mathematical operation. Let's break it down step-by-step:
- A number: This represents an unknown value, typically denoted by a variable like x, n, or y.
- Quotient of a number and 4: This means the result of dividing the number by 4. Algebraically, this is represented as x/4 or n ÷ 4.
- Five more than: This indicates adding 5 to the previous result.
Therefore, the complete expression "five more than the quotient of a number and 4" translates to: x/4 + 5 (or n ÷ 4 + 5). This is an algebraic expression, a combination of numbers, variables, and mathematical operations.
Translating Verbal Phrases into Algebraic Expressions
Understanding how to translate word problems into algebraic expressions is a fundamental skill in algebra. Here are some common phrases and their algebraic equivalents:
- Sum: Addition (+)
- Difference: Subtraction (-)
- Product: Multiplication (× or *)
- Quotient: Division (÷ or /)
- More than: Addition (+)
- Less than: Subtraction (-)
- Times: Multiplication (× or *)
- Divided by: Division (÷ or /)
Let's practice with a few examples:
- Eight more than a number:
x + 8 - The product of 6 and a number:
6x - Seven less than twice a number:
2x - 7 - The quotient of a number and 9, decreased by 2:
x/9 - 2 - Three times the sum of a number and 5:
3(x + 5)
Mastering these translations is crucial for solving various mathematical problems involving word problems.
Solving Problems Involving the Expression
Now, let's apply our understanding to solve problems involving the expression "five more than the quotient of a number and 4":
Problem 1: If the expression equals 7, what is the value of the number?
Solution:
We set up the equation: x/4 + 5 = 7
- Subtract 5 from both sides:
x/4 = 2 - Multiply both sides by 4:
x = 8
Therefore, the number is 8.
Problem 2: If the number is 12, what is the value of the expression?
Solution:
Substitute x with 12 in the expression: 12/4 + 5
- Divide 12 by 4:
3 + 5 - Add 5:
8
The value of the expression is 8.
Problem 3: A rectangle's length is five more than the quotient of its width and 4. If the width is 20, find the length.
Solution: Here, the width is analogous to our 'number' (x). We plug 20 into the expression:
20/4 + 5 = 10
The length of the rectangle is 10.
Extending the Concept: More Complex Scenarios
We can extend this concept to more complex scenarios by incorporating additional variables, operations, or even functions.
Scenario 1: Introducing a Second Variable:
Let's say the expression is "five more than the quotient of a number and another number, y." This translates to: x/y + 5. Now, we need two values, x and y, to evaluate the expression.
Scenario 2: Incorporating Exponents:
Consider "five more than the quotient of a number squared and 4": x²/4 + 5. The addition of the exponent introduces a new layer of complexity.
Scenario 3: Functional Representation:
We can define a function, f(x), representing the expression: f(x) = x/4 + 5. This allows us to input different values of x and obtain the corresponding output. We can then analyze the properties of this function, such as its domain, range, and graph.
Real-World Applications
This seemingly simple mathematical expression has real-world applications in various fields:
- Engineering: Calculating dimensions, material quantities, or ratios in construction or design.
- Finance: Determining average returns, calculating interest rates, or modeling investment growth.
- Physics: Solving problems related to speed, distance, time, or force.
- Computer Science: Developing algorithms and solving programming problems.
The ability to translate real-world problems into mathematical expressions like this one is a crucial skill for problem-solving in various disciplines.
Practical Exercises
To solidify your understanding, try these exercises:
- Translate the following phrases into algebraic expressions:
- Ten less than the quotient of a number and 3.
- The sum of a number and 7, divided by 2.
- Twice the difference of a number and 5.
- Solve for x in the equation:
x/5 + 3 = 8 - If the expression
x/6 + 4equals 7, what is the value of x? - A garden's length is five more than the quotient of its width and 2. If the width is 16, what is the length?
- Create your own word problem using the expression "five more than the quotient of a number and 4," and solve it.
Conclusion
The seemingly simple phrase "five more than the quotient of a number and 4" provides a gateway to understanding the power of algebraic expressions. By mastering the translation from verbal descriptions to algebraic notation and applying the fundamental principles of algebra, we can solve a wide range of problems and unlock the potential for more complex mathematical explorations in various fields. The ability to translate real-world problems into these types of expressions is invaluable for problem-solving and critical thinking. Remember to practice regularly and apply this knowledge to diverse scenarios to truly master the concept.
Latest Posts
Latest Posts
-
A Bar Magnet Is Placed In A Uniform Magnetic Field
Apr 05, 2025
-
Balance Equation Naoh H2so4 Na2so4 H2o
Apr 05, 2025
-
Non Metal Liquid At Room Temp
Apr 05, 2025
-
Which Of The Following Is An Example Of Pollution
Apr 05, 2025
-
Which Of The Following Is Not Characteristic Of Metals
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Five More Than The Quotient Of A Number And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
