A Bar Magnet Is Placed In A Uniform Magnetic Field
News Leon
Apr 05, 2025 · 6 min read
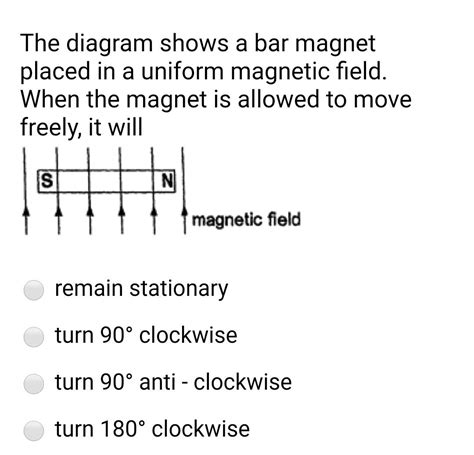
Table of Contents
A Bar Magnet in a Uniform Magnetic Field: Exploring Forces, Torques, and Potential Energy
The interaction between a bar magnet and a uniform magnetic field provides a fundamental illustration of magnetic phenomena. Understanding this interaction is crucial in various applications, from electric motors to magnetic resonance imaging (MRI). This article delves deep into the physics behind this interaction, exploring the forces, torques, and potential energy involved. We'll examine different orientations of the bar magnet within the field and analyze the resulting effects.
Understanding the Fundamentals
Before we explore the complexities of a bar magnet in a uniform magnetic field, let's review some basic concepts:
What is a Uniform Magnetic Field?
A uniform magnetic field is a region of space where the magnetic field vector (B) has the same magnitude and direction at every point. Imagine a perfectly aligned set of magnetic field lines – parallel and equally spaced. While truly uniform fields are difficult to achieve in practice, many experimental setups approximate this condition, allowing us to study the interactions effectively.
The Magnetic Dipole Moment
A bar magnet acts as a magnetic dipole, possessing a magnetic dipole moment (μ). This vector quantity represents the strength and orientation of the magnet's magnetic field. Its magnitude is typically proportional to the product of the pole strength and the distance between the poles. The direction of μ points from the south pole to the north pole of the magnet.
Magnetic Force and Torque
When a magnetic dipole is placed in a magnetic field, two primary effects are observed: a force and a torque. The force attempts to move the dipole, while the torque attempts to rotate it.
The Bar Magnet in a Uniform Field: Analyzing the Forces
In a perfectly uniform magnetic field, there is no net force acting on a magnetic dipole. This is because the magnetic forces on the north and south poles of the magnet are equal in magnitude and opposite in direction. These forces cancel each other out, resulting in zero net translational motion.
Think of it this way: the field exerts a force on each pole – one pole is pulled in one direction, and the other is pulled equally in the opposite direction. The forces are perfectly balanced.
This is a key difference compared to placing the magnet in a non-uniform field. In a non-uniform field, the forces on the poles will not be perfectly balanced, leading to a net force on the magnet and subsequent translational movement.
The Bar Magnet in a Uniform Field: Analyzing the Torques
The absence of a net force doesn't mean the bar magnet remains stationary. The most significant effect in a uniform field is the torque. This torque arises from the forces acting on the poles of the magnet, creating a rotational effect.
The magnitude of the torque (τ) experienced by the dipole is given by:
τ = μB sin θ
where:
- τ is the torque vector
- μ is the magnetic dipole moment vector
- B is the magnetic field vector
- θ is the angle between the magnetic dipole moment vector and the magnetic field vector.
This equation highlights a crucial aspect: the torque is maximum when the angle θ is 90 degrees (the magnetic dipole moment is perpendicular to the field), and zero when θ is 0 or 180 degrees (the magnetic dipole moment is aligned or anti-aligned with the field).
Understanding the Torque's Effect
The torque causes the magnet to rotate. If the magnet is initially not aligned with the magnetic field, it will experience a torque that tends to align its dipole moment with the field. This alignment is the lowest energy state for the system.
Imagine a compass needle in Earth's magnetic field. The torque aligns the needle with the Earth's field lines, pointing north.
The rotation continues until the magnet is aligned with the magnetic field. At this point, the torque becomes zero, and the magnet remains stable.
Potential Energy of a Magnetic Dipole in a Uniform Field
The potential energy (U) associated with a magnetic dipole in a uniform magnetic field is given by:
U = -μB cos θ
This equation reveals that:
- The potential energy is minimum (most stable) when θ = 0 (magnet aligned with the field).
- The potential energy is maximum (least stable) when θ = 180 degrees (magnet anti-aligned with the field).
- The potential energy is zero when θ = 90 degrees (magnet perpendicular to the field).
This potential energy landscape drives the magnet's tendency to align with the field – the system seeks the lowest energy state possible.
Practical Applications and Examples
The principles discussed above have numerous applications in various fields:
Electric Motors
Electric motors utilize the torque generated on a magnetic dipole in a magnetic field. The rotating coil of wire (which acts as a magnetic dipole) experiences a torque due to its interaction with the motor's permanent magnets or electromagnets. This torque causes the motor shaft to rotate, converting electrical energy into mechanical energy.
Magnetic Resonance Imaging (MRI)
MRI machines utilize strong, uniform magnetic fields to align the magnetic moments of atomic nuclei within the patient's body. By manipulating these aligned moments using radio waves, the machine generates images providing detailed information about the internal structures. The uniform field ensures consistent alignment throughout the imaging area.
Magnetic Compass
A simple yet powerful application is the magnetic compass. The Earth's magnetic field is approximately uniform over a small area. The compass needle, a small bar magnet, aligns itself with this field, indicating the direction of magnetic north.
Beyond the Uniform Field: A Look into Non-Uniform Fields
While this article focuses on uniform fields, it's crucial to acknowledge the differences when dealing with non-uniform magnetic fields. In a non-uniform field, the forces on the magnet's poles are unequal, leading to a net force acting on the magnet, in addition to the torque. This results in both translational and rotational motion. This is a significantly more complex scenario requiring vector calculus for thorough analysis. The forces and torques depend on the gradient of the magnetic field, meaning the rate of change of the field strength and direction.
For example, consider a magnet placed near a strong permanent magnet. The non-uniform field of the permanent magnet exerts a force on the bar magnet, pulling or repelling it depending on their respective orientations.
Conclusion
The behavior of a bar magnet in a uniform magnetic field provides a fundamental understanding of magnetic interactions. While seemingly simple, the concepts of force, torque, and potential energy are crucial for understanding numerous applications, from electric motors to medical imaging. The absence of net force, coupled with the rotational torque that strives for alignment with the field, showcases the elegance and significance of magnetic dipoles interacting with uniform fields. Further exploration into non-uniform fields reveals even richer dynamics and showcases the breadth and depth of magnetic phenomena. This understanding forms the cornerstone for many technological advancements and continues to inspire new discoveries in physics and engineering.
Latest Posts
Latest Posts
-
What Is The Solvent For Salt Water
Apr 06, 2025
-
The Most Commonly Used Measure Of Central Tendency Is The
Apr 06, 2025
-
A Covalent Bond Is Formed As The Result Of
Apr 06, 2025
-
Sales Revenues Are Usually Considered Earned When
Apr 06, 2025
-
Can A Homogeneous Mixture Be Separated
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about A Bar Magnet Is Placed In A Uniform Magnetic Field . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
