Determine The Value Of X In The Figure
News Leon
Mar 28, 2025 · 6 min read
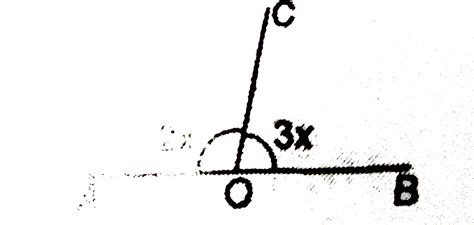
Table of Contents
Determining the Value of x: A Comprehensive Guide to Geometric Problem Solving
Determining the value of 'x' in a geometric figure is a fundamental skill in mathematics, crucial for various applications from simple geometry problems to complex engineering calculations. This comprehensive guide will explore various methods and techniques used to solve for 'x' in different geometric contexts, focusing on building a strong understanding of the underlying principles. We'll cover a range of scenarios, from simple equations involving angles and lengths to more complex problems requiring the application of theorems and properties of shapes.
Understanding the Fundamentals: Angles and Lines
Before delving into complex geometric problems, it's essential to have a strong grasp of fundamental concepts related to angles and lines. These form the bedrock upon which more complex solutions are built.
Types of Angles:
- Acute Angle: An angle measuring less than 90 degrees.
- Right Angle: An angle measuring exactly 90 degrees.
- Obtuse Angle: An angle measuring more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle measuring exactly 180 degrees.
- Reflex Angle: An angle measuring more than 180 degrees but less than 360 degrees.
Understanding these angle types is critical for solving problems involving angles in geometric figures. Many problems rely on the relationships between these angles, such as supplementary angles (adding up to 180 degrees) and complementary angles (adding up to 90 degrees).
Types of Lines:
- Parallel Lines: Lines that never intersect, maintaining a constant distance apart.
- Perpendicular Lines: Lines that intersect at a right angle (90 degrees).
- Intersecting Lines: Lines that cross each other at a point.
The relationships between parallel lines and transversals (lines intersecting parallel lines) are particularly important, leading to concepts like alternate interior angles, alternate exterior angles, corresponding angles, and consecutive interior angles – all of which are equal or supplementary in specific configurations.
Solving for 'x': Basic Geometric Shapes
Let's start with some basic geometric shapes and how to determine the value of 'x' within them.
Triangles:
Triangles are fundamental geometric shapes. The sum of interior angles in any triangle always equals 180 degrees. This property allows us to solve for 'x' if we know the values of two other angles.
Example: A triangle has angles measuring 70 degrees and 50 degrees. What is the value of the third angle, 'x'?
Solution: x = 180 - 70 - 50 = 60 degrees.
Isosceles Triangles: In an isosceles triangle, two sides and their corresponding angles are equal. Knowing this property can help solve for 'x' if the value of one angle or side is known.
Equilateral Triangles: All sides and angles in an equilateral triangle are equal. Each angle measures 60 degrees.
Quadrilaterals:
Quadrilaterals are four-sided polygons. The sum of interior angles in any quadrilateral is 360 degrees. Specific types of quadrilaterals have additional properties:
- Rectangles: Have four right angles (90 degrees each).
- Squares: Have four equal sides and four right angles.
- Parallelograms: Opposite sides are parallel and equal in length. Opposite angles are also equal.
- Rhombuses: Have four equal sides.
- Trapezoids: Have at least one pair of parallel sides.
Understanding these properties allows us to solve for 'x' based on the given information about the quadrilateral.
Solving for 'x': Advanced Geometric Concepts
Moving beyond basic shapes, let's explore more advanced geometric concepts and their application in solving for 'x'.
Similar Triangles:
Similar triangles have the same shape but different sizes. Their corresponding angles are equal, and their corresponding sides are proportional. This property is invaluable for solving problems involving similar triangles, allowing us to set up ratios to find unknown lengths or angles.
Example: Two similar triangles have sides of 3, 4, and 5 in one triangle and 6, 8, and 'x' in the other. Find the value of 'x'.
Solution: The ratio of corresponding sides is 2:1 (6/3 = 8/4 = 2). Therefore, x = 5 * 2 = 10.
Pythagorean Theorem:
The Pythagorean theorem applies to right-angled triangles. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is crucial for solving problems involving right-angled triangles where we need to find the length of an unknown side.
Example: A right-angled triangle has sides of length 3 and 4. What is the length of the hypotenuse, 'x'?
Solution: x² = 3² + 4² = 9 + 16 = 25. Therefore, x = √25 = 5.
Circles and Angles:
Circles introduce new relationships involving angles and arcs. Understanding concepts like central angles, inscribed angles, and angles formed by tangents and chords is vital for solving problems involving circles.
- Central Angle: An angle whose vertex is at the center of the circle. The measure of a central angle is equal to the measure of the intercepted arc.
- Inscribed Angle: An angle whose vertex is on the circle. The measure of an inscribed angle is half the measure of its intercepted arc.
Solving for 'x': Strategic Problem-Solving Techniques
Successfully determining the value of 'x' often requires a strategic approach to problem-solving. Here are some key techniques:
- Identify the type of geometric figure: Understanding the properties of the specific shape (triangle, quadrilateral, circle, etc.) is crucial.
- Analyze the given information: Carefully examine the provided values and relationships.
- Apply relevant theorems and properties: Utilize theorems like the Pythagorean theorem or properties of similar triangles.
- Draw diagrams: Visual representations can significantly aid in understanding the problem.
- Use algebraic equations: Set up equations based on the given information and solve for 'x'.
- Check your answer: Ensure your solution is reasonable and consistent with the given information.
Practice Problems: Testing Your Understanding
To solidify your understanding, let's work through some practice problems:
Problem 1: A triangle has angles measuring x, 2x, and 3x. Find the value of x.
Problem 2: A rectangle has a length of 10 and a width of x. Its diagonal measures 12. Find the value of x.
Problem 3: Two similar triangles have corresponding sides of 5 and 10. If one triangle has an area of 25 square units, what is the area of the other triangle?
Problem 4: A circle has a radius of 5. What is the length of an arc subtended by a central angle of 60 degrees?
Conclusion: Mastering Geometric Problem Solving
Determining the value of 'x' in geometric figures requires a solid understanding of fundamental geometric principles and a strategic approach to problem-solving. By mastering the techniques and concepts outlined in this guide, you'll develop the skills to tackle a wide range of geometric problems, building a strong foundation for more advanced mathematical studies and applications in various fields. Remember to practice regularly and always approach problems methodically to achieve success. The more practice you get, the more intuitive and efficient your problem-solving will become. Keep exploring geometric concepts, and your ability to solve for 'x' will continue to improve.
Latest Posts
Latest Posts
-
Most Lipid Digestion Occurs In The
Mar 31, 2025
-
Wheat Is A Monocot Or Dicot
Mar 31, 2025
-
What Is In Car Battery Acid
Mar 31, 2025
-
The Only Movable Joint In The Skull Is Between The
Mar 31, 2025
-
Which Inequality Is Shown In The Graph Below
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Determine The Value Of X In The Figure . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
