Classify The Following Triangle As Acute Obtuse Or Right Apex
News Leon
Apr 04, 2025 · 5 min read
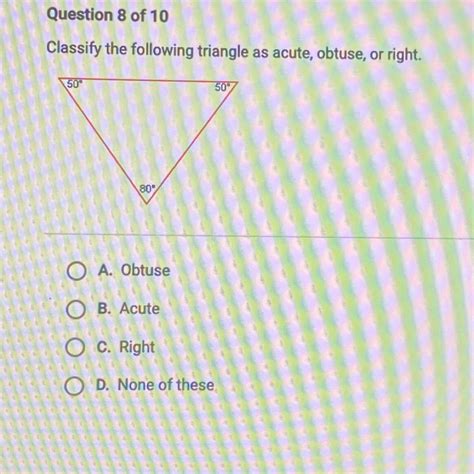
Table of Contents
Classifying Triangles: Acute, Obtuse, or Right
Understanding the classification of triangles based on their angles is fundamental to geometry. This comprehensive guide delves into the specifics of classifying triangles as acute, obtuse, or right, providing you with a clear understanding of the definitions, properties, and methods for determining the type of triangle you're working with. We'll explore various approaches, from examining angle measures to utilizing the Pythagorean theorem and its converse.
Defining the Triangle Types
Before we dive into the classification process, let's establish the definitions of each triangle type:
1. Acute Triangle: An acute triangle is a triangle where all three angles are acute angles – meaning each angle measures less than 90 degrees. The sum of the angles in any triangle always equals 180 degrees; therefore, in an acute triangle, each angle contributes to this sum with a value strictly less than 90 degrees.
2. Obtuse Triangle: An obtuse triangle has one obtuse angle – an angle measuring greater than 90 degrees. Since the sum of the angles must still be 180 degrees, the other two angles in an obtuse triangle must be acute angles.
3. Right Triangle: A right triangle contains one right angle – an angle measuring exactly 90 degrees. The other two angles in a right triangle are always acute angles and complement each other, meaning their sum is 90 degrees.
Methods for Classifying Triangles
Several methods exist to classify a triangle as acute, obtuse, or right. These methods vary in their applicability depending on the information provided.
1. Using Angle Measures: The Most Direct Approach
The simplest and most direct method is to examine the measures of the three angles.
- If all three angles are less than 90 degrees: The triangle is acute.
- If one angle is greater than 90 degrees: The triangle is obtuse.
- If one angle is exactly 90 degrees: The triangle is right.
This method is straightforward when the angle measures are explicitly given. However, you often need to deduce angle measures from other provided information.
2. Using the Pythagorean Theorem and its Converse for Right Triangles
The Pythagorean theorem is a cornerstone of geometry and provides a powerful tool for identifying right triangles. The theorem states: In a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus).
Pythagorean Theorem: a² + b² = c² (where 'c' is the hypotenuse)
The converse of the Pythagorean theorem is equally important for classification: If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Applying the Converse: Let's say we have a triangle with sides of length a, b, and c (where c is the longest side). If a² + b² = c², then the triangle is a right triangle. If a² + b² > c², then the triangle is acute. If a² + b² < c², then the triangle is obtuse.
This method is particularly useful when you know the lengths of the triangle's sides but not the angle measures.
3. Using the Law of Cosines
The Law of Cosines is a more general theorem that can be used to find the measure of any angle in a triangle, given the lengths of all three sides. The formula is:
c² = a² + b² - 2ab * cos(C)
Where:
- a, b, and c are the lengths of the sides.
- C is the angle opposite side c.
By solving for cos(C), you can determine the measure of angle C. You can then apply the angle measure classification method described earlier. This method is versatile but requires more calculation than the Pythagorean theorem's converse.
Examples of Classifying Triangles
Let's illustrate these methods with some examples:
Example 1: A triangle has angles measuring 60°, 60°, and 60°.
Classification: Since all angles are less than 90°, this is an acute triangle. It's also an equilateral triangle because all angles and sides are equal.
Example 2: A triangle has angles measuring 30°, 60°, and 90°.
Classification: The presence of a 90° angle clearly indicates this is a right triangle. This is also a special right triangle known as a 30-60-90 triangle.
Example 3: A triangle has angles measuring 20°, 110°, and 50°.
Classification: The presence of an angle greater than 90° (110°) makes this an obtuse triangle.
Example 4: A triangle has sides of length 3, 4, and 5.
Classification: Let's apply the Pythagorean theorem's converse: 3² + 4² = 9 + 16 = 25 5² = 25 Since 3² + 4² = 5², this is a right triangle.
Example 5: A triangle has sides of length 5, 6, and 7.
Classification: Applying the Pythagorean theorem's converse: 5² + 6² = 25 + 36 = 61 7² = 49 Since 5² + 6² > 7², this is an acute triangle.
Example 6: A triangle has sides of length 2, 3, and 5.
Classification: Applying the Pythagorean theorem's converse: 2² + 3² = 4 + 9 = 13 5² = 25 Since 2² + 3² < 5², this is an obtuse triangle.
Advanced Considerations and Applications
The classification of triangles isn't just an academic exercise. Understanding these classifications is crucial in various fields:
-
Engineering: The properties of different triangle types significantly impact structural design. Right triangles, for example, are frequently used in building frameworks due to their stability.
-
Computer Graphics: Triangle classification is fundamental in computer graphics and 3D modeling. Understanding the angles and properties of triangles is essential for rendering and manipulating 3D objects accurately.
-
Trigonometry: Many trigonometric functions and identities are specifically defined for right-angled triangles.
-
Cartography: Triangles are used extensively in surveying and mapmaking. Understanding their properties helps ensure accuracy in measurements and calculations.
-
Physics: Numerous physical phenomena and calculations rely on geometric principles, including triangle classifications.
Conclusion
Classifying triangles as acute, obtuse, or right is a foundational concept in geometry. Mastering the various methods presented in this guide will empower you to solve a wide range of geometric problems efficiently. By understanding the definitions, theorems, and application methods, you'll be well-equipped to approach any triangle classification challenge with confidence. Remember, practice is key to solidifying your understanding and developing your problem-solving skills. Work through numerous examples, applying different methods to reinforce your learning. This will not only improve your understanding of triangle classifications but also enhance your overall geometric reasoning abilities.
Latest Posts
Latest Posts
-
How Many Unpaired Electrons Does A Sulfur Atom Have
Apr 04, 2025
-
Bromine Is A Metal Or Nonmetal
Apr 04, 2025
-
Coefficient Of Linear Expansion Of Iron
Apr 04, 2025
-
A Solution Of H2so4 With A Molal Concentration Of 5 25
Apr 04, 2025
-
What Is Another Name For A Living Thing
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Classify The Following Triangle As Acute Obtuse Or Right Apex . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
