Circumference Of A Circle With A Radius Of 3
News Leon
Mar 30, 2025 · 5 min read
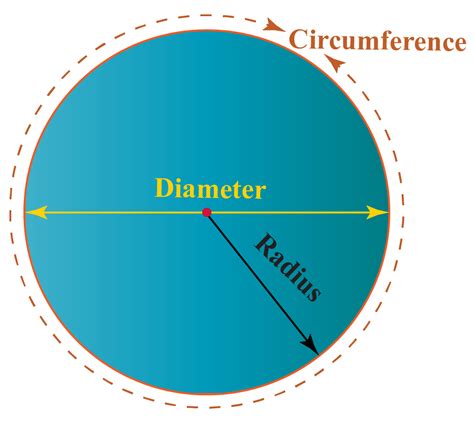
Table of Contents
Circumference of a Circle with a Radius of 3: A Comprehensive Exploration
The seemingly simple question of finding the circumference of a circle with a radius of 3 units opens a door to a fascinating exploration of mathematical concepts, their applications, and the elegance of geometric relationships. This article delves deep into this seemingly straightforward problem, examining the underlying formula, exploring variations and related concepts, and even touching upon its practical applications in various fields.
Understanding the Fundamentals: Circumference and Radius
Before we jump into calculating the circumference of our circle, let's define the key terms.
-
Circumference: The circumference of a circle is the distance around its edge. Imagine wrapping a string around a circular object; the length of that string represents the circumference. It's a linear measurement, usually expressed in units of length like centimeters, meters, inches, or feet.
-
Radius: The radius of a circle is the distance from the center of the circle to any point on its edge. It's half the diameter. In our case, the radius is given as 3 units.
-
Diameter: The diameter is a straight line passing through the center of the circle and connecting two points on the opposite edges. It's twice the length of the radius. For our circle, the diameter would be 2 * 3 = 6 units.
The Formula: Pi and its Significance
The cornerstone of calculating a circle's circumference is the mathematical constant π (pi). Pi represents the ratio of a circle's circumference to its diameter. It's an irrational number, meaning its decimal representation goes on forever without repeating. Its approximate value is 3.14159, although more precise values are used in scientific and engineering calculations.
The formula for the circumference (C) of a circle is:
C = 2πr
where:
- C = Circumference
- π = Pi (approximately 3.14159)
- r = Radius
Calculating the Circumference: A Step-by-Step Guide
Now, let's apply the formula to our circle with a radius of 3 units:
C = 2π(3)
C = 6π
This is the exact circumference. To get an approximate numerical value, we can substitute an approximate value for π:
C ≈ 6 * 3.14159
C ≈ 18.84954 units
Therefore, the circumference of a circle with a radius of 3 units is approximately 18.85 units. The precision of the result depends on the number of decimal places used for π.
Beyond the Basics: Exploring Variations and Applications
While the basic calculation is straightforward, understanding the implications and applications of the circumference formula expands its significance.
1. Circumference using Diameter
The circumference can also be calculated using the diameter (d) instead of the radius:
C = πd
Since the diameter is twice the radius (d = 2r), this formula is equivalent to the radius-based formula. For our circle, using the diameter (6 units), we get:
C = π * 6
C ≈ 18.84954 units
This reinforces the interchangeable nature of the two formulas.
2. Finding the Radius from the Circumference
If we know the circumference, we can work backward to find the radius. Rearranging the formula C = 2πr, we get:
r = C / 2π
This allows us to determine the radius of any circle if its circumference is known.
3. Applications in Real-World Scenarios
The concept of circumference has countless real-world applications:
- Engineering: Calculating the amount of material needed for circular structures like pipes, wheels, and gears.
- Construction: Determining the perimeter of circular foundations, pools, or gardens.
- Manufacturing: Designing and manufacturing circular components for various machines and products.
- Cartography: Calculating distances on maps involving circular regions or arcs.
- Astronomy: Estimating the size of celestial bodies or the distances they travel in orbits.
4. Circumference in More Complex Shapes
The concept of circumference extends beyond simple circles. Consider the circumference of a semi-circle, which is half the circumference of a full circle plus the diameter. Or consider the arc length of a sector of a circle, which is a proportional part of the full circumference.
5. Advanced Concepts: Circular Motion and Angular Velocity
In physics and engineering, circumference plays a vital role in understanding circular motion. The circumference is directly related to the distance covered by an object moving in a circular path. This is crucial for calculating angular velocity, which measures the rate of rotation of an object around a central axis.
6. Relationship to Area: A Comparative Look
While this article focuses on circumference, it's worth briefly mentioning the area of a circle. The formula for the area (A) of a circle is:
A = πr²
Comparing the formulas for circumference and area reveals an interesting relationship between the linear and the area measurements of a circle. Both depend on the radius, but the area involves the radius squared, indicating a non-linear relationship.
Expanding the Knowledge: Further Exploration
The exploration of circles and their properties doesn't end here. Here are some avenues for further investigation:
- Advanced Geometry: Delve deeper into concepts like radians, arc lengths, and sector areas.
- Trigonometry: Explore how trigonometric functions relate to circles and their properties.
- Calculus: Understand how calculus can be used to derive the formulas for circumference and area.
- History of Pi: Research the fascinating history of Pi and its discovery throughout the ages.
Conclusion: The Enduring Significance of a Simple Formula
The seemingly simple calculation of the circumference of a circle with a radius of 3 units serves as a gateway to a rich tapestry of mathematical concepts and their practical applications. From understanding fundamental geometric relationships to exploring advanced concepts in physics and engineering, the circumference formula remains a cornerstone of mathematical knowledge. Its enduring significance lies not just in its computational simplicity but also in its wide-ranging implications across various fields of study and application. The next time you encounter a circle, remember the elegance and power inherent in this fundamental formula.
Latest Posts
Latest Posts
-
What Is The Formula Of Iq
Apr 01, 2025
-
A Path That An Electric Current Follows Is A
Apr 01, 2025
-
Distance From Earth To Sun Scientific Notation
Apr 01, 2025
-
The Chromosomes Are Aligned At The Spindle Equator During
Apr 01, 2025
-
Integers Are A Subset Of Rational Numbers True False
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Circumference Of A Circle With A Radius Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
