Choose The Equation That Represents The Graph
News Leon
Mar 29, 2025 · 6 min read
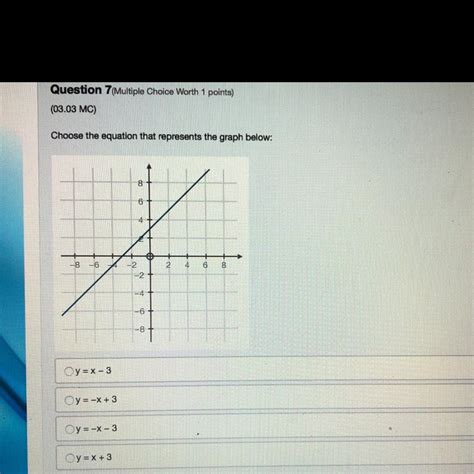
Table of Contents
Choose the Equation That Represents the Graph: A Comprehensive Guide
Choosing the correct equation to represent a given graph is a fundamental skill in algebra and numerous other mathematical disciplines. This ability is crucial for understanding relationships between variables, predicting future outcomes, and building mathematical models for real-world scenarios. This comprehensive guide will equip you with the tools and techniques necessary to confidently tackle this challenge, covering various graph types and their corresponding equations. We will explore linear equations, quadratic equations, exponential equations, and logarithmic equations, examining their unique characteristics and how to identify them from their graphical representations.
Understanding the Basics: Variables and Relationships
Before diving into specific equation types, let's establish a foundational understanding. A graph visually depicts the relationship between two or more variables. The horizontal axis (x-axis) typically represents the independent variable, while the vertical axis (y-axis) represents the dependent variable. The equation representing the graph mathematically defines this relationship, allowing us to calculate the value of the dependent variable (y) for any given value of the independent variable (x).
Key Features to Identify:
Before attempting to choose the correct equation, carefully analyze the graph for key features. These features act as visual clues that will significantly narrow down the possibilities. Consider the following:
- Linearity: Does the graph form a straight line? If so, it represents a linear equation.
- Curvature: Does the graph curve? If it curves upwards, it might be a quadratic or exponential function. A curve that increases at a decreasing rate could indicate a logarithmic function.
- Intercepts: What are the x-intercept (where the graph crosses the x-axis) and the y-intercept (where the graph crosses the y-axis)? These intercepts provide valuable information about the equation.
- Asymptotes: Does the graph approach a horizontal or vertical line without ever touching it? These lines are called asymptotes, and their presence often indicates exponential or logarithmic functions.
- Symmetry: Is the graph symmetrical about the y-axis, the x-axis, or the origin? Symmetry can provide significant clues about the type of equation.
- Slope: For linear graphs, determine the slope (the steepness of the line). The slope is the ratio of the vertical change to the horizontal change between any two points on the line.
Identifying Equations from Graph Types
Let's explore the common types of equations and their corresponding graphical representations.
1. Linear Equations: y = mx + c
Linear equations represent a straight-line relationship between two variables. The general form is y = mx + c, where:
- m represents the slope (the steepness of the line). A positive slope indicates an upward-sloping line, while a negative slope indicates a downward-sloping line. A slope of zero indicates a horizontal line.
- c represents the y-intercept (the point where the line crosses the y-axis).
How to identify from a graph: Look for a straight line. Calculate the slope using two points on the line: m = (y2 - y1) / (x2 - x1). The y-intercept is the y-coordinate where the line crosses the y-axis.
2. Quadratic Equations: y = ax² + bx + c
Quadratic equations represent a parabolic curve. The general form is y = ax² + bx + c, where:
- a, b, and c are constants.
- The sign of a determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
- The vertex of the parabola is the point where the curve changes direction.
How to identify from a graph: Look for a U-shaped or inverted U-shaped curve. The vertex represents the minimum or maximum value of the function.
3. Exponential Equations: y = abˣ
Exponential equations represent a curve that increases or decreases rapidly. The general form is y = abˣ, where:
- a is the initial value (the y-intercept).
- b is the base, which determines the rate of growth or decay. If b > 1, the function grows exponentially. If 0 < b < 1, the function decays exponentially.
How to identify from a graph: Look for a curve that increases or decreases rapidly, approaching a horizontal asymptote (a horizontal line that the curve gets closer to but never touches).
4. Logarithmic Equations: y = logₐx
Logarithmic equations represent the inverse of exponential functions. The general form is y = logₐx, where:
- a is the base of the logarithm. The most common base is 10 (common logarithm) or e (natural logarithm, denoted as ln x).
How to identify from a graph: Look for a curve that increases slowly at first, then increases more rapidly. It approaches a vertical asymptote (a vertical line that the curve gets closer to but never touches).
Advanced Techniques and Considerations
In more complex scenarios, identifying the equation might require a combination of techniques and a deeper understanding of mathematical properties.
1. Using Multiple Points:
If the graph doesn't clearly reveal the type of equation, you can use multiple points on the graph to solve a system of equations. For example, if you suspect a quadratic equation, you can substitute the coordinates of three points into the general form (y = ax² + bx + c) to obtain three equations with three unknowns (a, b, and c). Solving this system will give you the specific equation.
2. Transformations of Functions:
Graphs can be transformations of basic functions (like shifting, stretching, or reflecting). Identifying these transformations can help in determining the equation. For instance, if a graph is a parabola shifted to the right and up, you can modify the basic quadratic equation (y = x²) to reflect these transformations.
3. Utilizing Technology:
Graphing calculators and software can be powerful tools for analyzing graphs and determining their equations. Many software packages offer curve-fitting capabilities that can estimate the equation based on a set of data points. However, it is always best to develop your own understanding of the processes involved, rather than relying solely on technology.
Practical Examples
Let's illustrate these techniques with some examples.
Example 1: A graph shows a straight line passing through points (1, 2) and (3, 6).
- Solution: Calculate the slope: m = (6 - 2) / (3 - 1) = 2.
- The equation is of the form y = 2x + c. Substitute one point (e.g., (1, 2)) to find c: 2 = 2(1) + c => c = 0.
- Therefore, the equation is y = 2x.
Example 2: A graph shows a parabola opening upwards with a vertex at (2, 1) and passing through the point (3, 3).
- Solution: Since the parabola opens upwards, the equation is of the form y = a(x - h)² + k, where (h, k) is the vertex.
- Substituting the vertex, we get y = a(x - 2)² + 1.
- Substitute the point (3, 3) to find 'a': 3 = a(3 - 2)² + 1 => a = 2.
- Therefore, the equation is y = 2(x - 2)² + 1.
Conclusion
Choosing the correct equation that represents a given graph involves a systematic approach. By carefully analyzing the graph's features, understanding the characteristics of different equation types, and employing appropriate techniques, you can confidently determine the mathematical relationship depicted. This skill is not only crucial for success in mathematics but also essential for various applications in science, engineering, and other fields. Remember to practice regularly, and your ability to decipher graphs and their corresponding equations will continuously improve. Mastering this skill empowers you to interpret and model the world around you through the language of mathematics.
Latest Posts
Latest Posts
-
Chemical Equations Must Be Balanced To Satisfy The
Mar 31, 2025
-
Melting Of Butter Is A Physical Change
Mar 31, 2025
-
Why Is Dna Replication Called A Semi Conservative Process
Mar 31, 2025
-
Osmosis Involves The Movement Of What Substance
Mar 31, 2025
-
Is 1 3 An Irrational Number
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Choose The Equation That Represents The Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
