At What Angle Is The Maximum Range In Projectile Motion
News Leon
Apr 05, 2025 · 5 min read
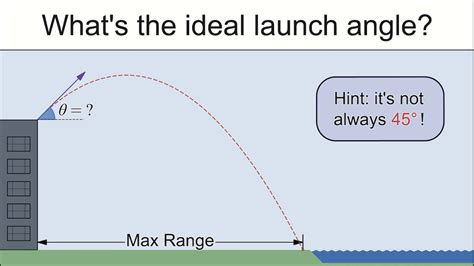
Table of Contents
At What Angle is the Maximum Range in Projectile Motion? A Deep Dive
Projectile motion, the curved path an object follows when launched into the air, is a fundamental concept in physics with wide-ranging applications from sports to aerospace engineering. Understanding projectile motion, particularly the angle that maximizes its range, is crucial for optimizing performance in many fields. This comprehensive article delves into the physics behind projectile motion, explains how the launch angle affects range, and explores the conditions under which maximum range is achieved.
Understanding Projectile Motion: The Basics
Before we delve into the specifics of maximum range, let's establish a foundational understanding of projectile motion. We assume, for simplicity, that air resistance is negligible. This allows us to focus on the core principles governed by gravity and initial velocity.
Key Factors Influencing Projectile Motion
Several factors significantly influence the trajectory of a projectile:
- Initial Velocity (v₀): This is the speed at which the projectile is launched. A higher initial velocity generally leads to a greater range.
- Launch Angle (θ): This is the angle between the initial velocity vector and the horizontal plane. The launch angle critically determines the range and maximum height achieved by the projectile.
- Acceleration due to Gravity (g): This is the constant downward acceleration caused by Earth's gravitational pull (approximately 9.8 m/s²).
Resolving Velocity Components
To analyze projectile motion effectively, we resolve the initial velocity into two independent components:
- Horizontal Component (v₀x): This component remains constant throughout the projectile's flight, assuming no air resistance. It's calculated as:
v₀x = v₀ * cos(θ) - Vertical Component (v₀y): This component changes constantly due to the influence of gravity. It's calculated as:
v₀y = v₀ * sin(θ)
These components allow for separate analysis of horizontal and vertical motion, simplifying calculations.
The Range Equation: Unveiling the Relationship Between Angle and Distance
The horizontal range (R) of a projectile, the total horizontal distance it travels before landing, can be expressed mathematically as:
R = (v₀² * sin(2θ)) / g
This equation reveals the crucial relationship between range (R), initial velocity (v₀), launch angle (θ), and acceleration due to gravity (g).
Notice: The range is directly proportional to the square of the initial velocity. Doubling the initial velocity quadruples the range!
Determining the Angle for Maximum Range
From the range equation, it's evident that the range is maximized when the term sin(2θ) is maximized. The sine function reaches its maximum value of 1 when its argument is 90 degrees. Therefore:
2θ = 90°
θ = 45°
Therefore, the maximum range of a projectile is achieved when the launch angle is 45 degrees. This holds true under the idealized conditions of negligible air resistance.
The Influence of Air Resistance: A Real-World Consideration
The previous analysis assumes a frictionless environment, which is rarely the case in the real world. Air resistance significantly affects projectile motion, especially at higher velocities and over longer distances.
How Air Resistance Affects Range
Air resistance acts as a force opposing the projectile's motion. This force is dependent on several factors, including:
- Velocity: The faster the projectile, the greater the air resistance.
- Shape and Size: A more aerodynamic shape experiences less air resistance.
- Air Density: Higher air density (e.g., at lower altitudes) increases air resistance.
Air resistance reduces both the horizontal and vertical components of velocity, leading to a shorter range and a lower maximum height. It also alters the optimal launch angle for maximum range. In the presence of air resistance, the optimal launch angle is slightly less than 45 degrees. The exact angle depends on the specific conditions.
Exploring Other Factors Affecting Projectile Motion
Besides air resistance and launch angle, other factors influence projectile motion:
- Gravity: The strength of gravity (g) varies slightly depending on location (altitude and latitude).
- Wind: Wind introduces a horizontal force, affecting the projectile's trajectory and range. Headwinds reduce range, while tailwinds increase it.
- Spin: The spin imparted to a projectile (e.g., a baseball or golf ball) can significantly influence its flight path due to the Magnus effect.
Practical Applications and Examples
Understanding the principles of projectile motion and the optimal launch angle has diverse practical applications:
- Sports: In sports like basketball, baseball, and long jump, athletes instinctively or through training, optimize their launch angles to achieve maximum range or distance.
- Military Applications: The trajectory of artillery shells and rockets is meticulously calculated based on launch angle, velocity, and other factors to achieve accurate target acquisition.
- Aerospace Engineering: The design of rockets and missiles involves precise control of trajectory and launch angles to maximize range and reach specific destinations.
Advanced Concepts and Further Exploration
This article provides a fundamental understanding of projectile motion and the angle for maximum range. For a more in-depth analysis, one can explore:
- Numerical Methods: Using computational methods to simulate projectile motion with air resistance for various scenarios.
- Advanced Calculus: Applying calculus to derive more complex equations that account for air resistance and other variables.
- Experimental Physics: Conducting experiments to measure the range and trajectory of projectiles under different conditions.
Conclusion: Mastering the Angle for Maximum Range
The 45-degree launch angle for maximum range is a foundational concept in projectile motion. While ideal conditions assume negligible air resistance, understanding this principle provides a valuable starting point for analyzing real-world scenarios. Accounting for air resistance and other factors necessitates more sophisticated models and calculations, but the fundamental relationship between launch angle and range remains a crucial element in diverse fields. This knowledge empowers professionals and enthusiasts alike to optimize performance and achieve desired results in various applications, from sports to advanced engineering.
Latest Posts
Latest Posts
-
Difference Between Diminished Image And Enlarged Image
Apr 06, 2025
-
Lymph Differs From Plasma In That
Apr 06, 2025
-
Chlorine Has Two Naturally Occurring Isotopes
Apr 06, 2025
-
What Is The Boiling Point In Kelvin
Apr 06, 2025
-
How Many Seconds In A Year In Scientific Notation
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about At What Angle Is The Maximum Range In Projectile Motion . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
