Area Of Circle With Radius Of 8
News Leon
Mar 30, 2025 · 5 min read
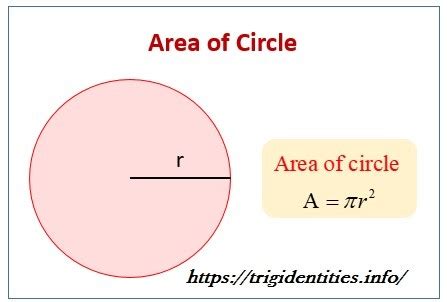
Table of Contents
Delving Deep into the Area of a Circle with Radius 8: A Comprehensive Guide
The seemingly simple concept of calculating the area of a circle hides a rich history and a surprising number of applications. This article delves deep into the calculation of the area of a circle with a radius of 8 units, exploring the underlying formula, practical applications, and even touching upon some historical context. We'll go beyond a simple answer, providing a robust understanding of the topic suitable for students, educators, and anyone curious about the fascinating world of geometry.
Understanding the Fundamental Formula: πr²
The area of any circle is given by the formula A = πr², where:
- A represents the area of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter and is an irrational number, meaning its decimal representation goes on forever without repeating.
- r represents the radius of the circle, which is the distance from the center of the circle to any point on its circumference.
This formula is fundamental to countless applications in mathematics, engineering, physics, and many other fields. It’s a cornerstone of geometry and a building block for more complex calculations.
Calculating the Area: A Step-by-Step Guide
For a circle with a radius of 8 units, the calculation is straightforward:
-
Identify the radius: We are given that the radius (r) = 8 units.
-
Substitute into the formula: We plug the radius value into the area formula: A = π(8)²
-
Square the radius: 8² = 64
-
Multiply by π: A = π * 64 ≈ 64 * 3.14159 ≈ 201.06176 square units.
Therefore, the area of a circle with a radius of 8 units is approximately 201.06 square units. The use of "approximately" is crucial here because π is an irrational number, and we're using a rounded approximation.
Beyond the Calculation: Practical Applications
The ability to calculate the area of a circle is far from a theoretical exercise. Its applications span numerous fields:
1. Engineering and Construction:
-
Circular structures: Calculating the area is essential for designing and constructing circular structures like water tanks, silos, and even roundabouts. Knowing the area allows engineers to determine the material needed, the volume capacity, and optimize the design for strength and efficiency.
-
Piping and plumbing: The cross-sectional area of pipes is crucial for determining flow rates of liquids or gases. Understanding the relationship between radius and area is vital for efficient system design.
-
Foundation design: Circular foundations require precise area calculations to ensure structural stability and appropriate load-bearing capacity.
2. Agriculture and Forestry:
-
Irrigation systems: Understanding circular areas helps optimize the coverage and efficiency of sprinkler systems for watering crops.
-
Forest management: Calculating the area of circular clearings or the area covered by a tree canopy can aid in sustainable forest management and conservation efforts.
3. Manufacturing and Design:
-
Packaging design: Companies use area calculations to determine the material needed for circular containers and packaging, minimizing waste and optimizing production costs.
-
Manufacturing parts: Circular components are common in many industries, and calculating the area helps determine the material requirements and manufacturing processes.
4. Everyday Life:
-
Pizza sizes: Comparing pizza sizes often involves comparing their areas. A larger pizza with a greater radius offers a substantially larger eating area.
-
Gardening: Designing circular flowerbeds or vegetable patches involves calculating the area to determine the amount of soil, plants, and other resources needed.
-
Circular swimming pools: Similar to other circular structures, the area calculation is critical for determining the amount of water required, the size of the surrounding deck, and safety considerations.
Exploring π: A Constant with a Rich History
The constant π has fascinated mathematicians and scientists for millennia. Its value has been approximated by various civilizations throughout history:
-
Ancient Babylonians: Used a value of approximately 3.125.
-
Ancient Egyptians: Employed a value close to 3.16.
-
Archimedes: In the 3rd century BC, Archimedes developed a method for approximating π using polygons inscribed and circumscribed within a circle, achieving a remarkably accurate approximation.
-
Modern approximations: Today, computers have calculated π to trillions of digits, though only a relatively small number of digits are needed for most practical applications.
The ongoing quest for more accurate approximations of π highlights its fundamental importance in mathematics and our understanding of the universe.
Advanced Concepts and Related Formulas
While the basic formula A = πr² suffices for many applications, understanding related concepts can be beneficial:
-
Circumference: The circumference (C) of a circle is the distance around it, given by the formula C = 2πr. Knowing both area and circumference provides a comprehensive understanding of the circle's dimensions.
-
Diameter: The diameter (d) of a circle is twice the radius (d = 2r). This simple relationship is crucial for converting between radius and diameter.
-
Sector Area: A sector is a portion of a circle enclosed by two radii and an arc. Its area is given by the formula A_sector = (θ/360°) * πr², where θ is the central angle of the sector in degrees.
-
Segment Area: A segment is the area between a chord and an arc of a circle. Calculating the area of a segment requires a more complex formula involving trigonometry.
Solving Related Problems: Putting it into Practice
Let's explore some example problems that build upon our understanding of the area of a circle with radius 8:
Problem 1: A circular garden has a radius of 8 meters. What is the area of the garden?
Solution: Using the formula A = πr², we calculate A = π(8)² ≈ 201.06 square meters.
Problem 2: A circular swimming pool has an area of approximately 201 square meters. What is its radius?
Solution: Rearranging the formula, we get r = √(A/π). Therefore, r ≈ √(201/π) ≈ 8 meters.
Problem 3: A circular pizza has a radius of 8 inches. If a slice represents a 30° sector, what is the area of the slice?
Solution: Using the sector area formula, A_sector = (30°/360°) * π(8)² ≈ 16.75 square inches.
Conclusion: Mastering the Area of a Circle
This comprehensive exploration has moved beyond a simple calculation to encompass the historical context, practical applications, and related concepts surrounding the area of a circle with a radius of 8 units. Understanding this seemingly basic formula is a crucial stepping stone for tackling more complex geometric problems and applying these principles in diverse fields. From engineering marvels to everyday scenarios, the ability to calculate and understand circular areas is a valuable skill with widespread implications. By mastering this concept, you unlock a deeper understanding of the world around us and its mathematical underpinnings.
Latest Posts
Latest Posts
-
Draw And Label A Ph Scale
Apr 01, 2025
-
Which Of The Following Are Characteristics Of A Competitive Market
Apr 01, 2025
-
An Indifference Curve Shows All Combinations Of Two Goods That
Apr 01, 2025
-
Which Cell Organelle Is The Site Of Cellular Respiration
Apr 01, 2025
-
Can A Plane Mirror Form A Real Image
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Area Of Circle With Radius Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
