Area Of A Circle With A Radius Of 7
News Leon
Mar 27, 2025 · 5 min read
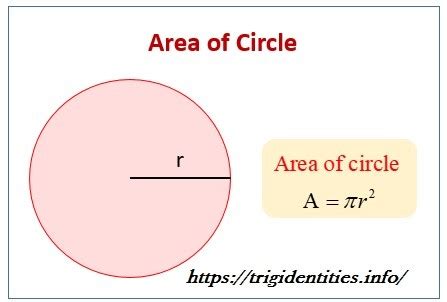
Table of Contents
Area of a Circle with a Radius of 7: A Comprehensive Guide
The seemingly simple question, "What is the area of a circle with a radius of 7?" opens a door to a fascinating exploration of geometry, mathematical formulas, and their practical applications. This comprehensive guide will delve deep into calculating the area, explore the underlying concepts, and demonstrate the versatility of this fundamental geometric principle.
Understanding the Fundamentals: Circles and Their Areas
Before we jump into the calculation, let's solidify our understanding of circles and their areas. A circle is a two-dimensional geometric shape defined as a set of points equidistant from a central point called the center. The distance from the center to any point on the circle is called the radius, often denoted by the letter 'r'. Twice the radius is the diameter, which passes through the center and connects two opposite points on the circle.
The area of a circle represents the amount of space enclosed within the circle's circumference. It's not just a theoretical concept; understanding the area of a circle is crucial in various fields, from engineering and architecture to designing clothing patterns and even planning urban landscapes.
The Formula: Pi and the Power of π
The formula for calculating the area of a circle is elegantly simple, yet profoundly impactful:
Area = πr²
Where:
- Area: Represents the area of the circle.
- π (Pi): Is a mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter and is an irrational number, meaning its decimal representation goes on forever without repeating. For practical purposes, we often use approximations like 3.14 or 3.14159.
- r² (Radius Squared): Is the radius of the circle multiplied by itself.
Calculating the Area: A Step-by-Step Guide (Radius = 7)
Now, let's apply the formula to calculate the area of a circle with a radius of 7 units (could be centimeters, inches, meters, etc.):
Step 1: Identify the radius.
In this case, the radius (r) is given as 7.
Step 2: Square the radius.
r² = 7² = 7 * 7 = 49
Step 3: Multiply by Pi (π).
Using the approximation of π ≈ 3.14159:
Area = π * r² = 3.14159 * 49 ≈ 153.938 square units
Therefore, the area of a circle with a radius of 7 units is approximately 153.938 square units.
Different Approximations of Pi and Their Impact
The accuracy of our calculation depends on the approximation of π we use. Let's compare results using different approximations:
- Using π ≈ 3.14: Area = 3.14 * 49 ≈ 153.86 square units
- Using π ≈ 3.14159: Area = 3.14159 * 49 ≈ 153.938 square units
- Using π ≈ 22/7: Area = (22/7) * 49 = 22 * 7 = 154 square units
As you can see, the difference between the approximations is relatively small, especially for circles with a relatively small radius. However, for larger circles or applications requiring high precision, using a more accurate approximation of π is crucial.
Beyond the Calculation: Real-World Applications
The seemingly simple calculation of a circle's area has far-reaching implications in various fields:
1. Engineering and Architecture:
- Designing circular structures: Calculating the area is fundamental in designing anything from water tanks and silos to roundabouts and stadium seating. Knowing the area helps determine material requirements, cost estimations, and space optimization.
- Pipe and conduit sizing: The cross-sectional area of pipes and conduits directly impacts their flow capacity. Accurate area calculations are essential for efficient fluid transport in various industries.
- Calculating land area: In surveying and land development, determining the area of circular plots is necessary for property valuation, zoning regulations, and construction planning.
2. Manufacturing and Production:
- Cutting circular materials: In industries like manufacturing and textiles, cutting circular shapes from sheets of metal, fabric, or wood requires precise area calculations to minimize waste and maximize efficiency.
- Designing gears and rotating parts: The area of circular components in machinery directly impacts their strength, durability, and overall performance.
- Packaging and labeling: Designing circular labels and containers necessitates accurate area calculations to ensure appropriate sizing and efficient packaging.
3. Science and Research:
- Calculating areas in microscopy: In biology and materials science, determining the area of cells, particles, or other circular structures is critical for analysis and research.
- Modeling circular phenomena: Many natural phenomena, like planetary orbits and wave patterns, involve circles. Understanding the area helps in modeling and analyzing these phenomena.
4. Everyday Life:
- Calculating pizza sizes: The area of a pizza directly relates to its size and the amount of pizza per slice.
- Designing gardens and landscapes: Circular flower beds, pools, or patio areas require area calculations for planning and design.
- Cooking and baking: Many recipes involve circular shapes, and knowing the area can help with ingredient proportions and cooking times.
Exploring Related Concepts: Circumference and Sector Area
Understanding the area of a circle opens the door to exploring related concepts:
1. Circumference:
The circumference of a circle is the distance around its edge. The formula for circumference is:
Circumference = 2πr
For a circle with a radius of 7, the circumference is approximately 2 * 3.14159 * 7 ≈ 43.98 units.
2. Sector Area:
A sector is a portion of a circle enclosed between two radii and an arc. The area of a sector is a fraction of the circle's total area, depending on the central angle of the sector. The formula is:
Sector Area = (θ/360°) * πr²
Where θ is the central angle in degrees.
Conclusion: The Enduring Significance of Circle Area
The seemingly simple calculation of the area of a circle with a radius of 7, yielding approximately 153.938 square units, is much more than just a mathematical exercise. It represents a fundamental concept with profound implications across various disciplines and everyday life. From engineering marvels to everyday cooking, understanding the area of a circle empowers us to solve practical problems, design efficiently, and analyze complex phenomena. Mastering this fundamental concept is a key step in developing a strong foundation in mathematics and its practical applications. The more we explore its applications, the more we appreciate its enduring significance.
Latest Posts
Latest Posts
-
What Sea Separates Europe From Africa
Mar 30, 2025
-
Charge Of Sodium Ion In Coulombs
Mar 30, 2025
-
Why Are Terrestrial Planets Denser Than Jovian Planets
Mar 30, 2025
-
Area Of Circle With Radius Of 8
Mar 30, 2025
-
Why Is Blood Considered Connective Tissue
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Area Of A Circle With A Radius Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
