All Whole Numbers Are Natural Numbers True Or False
News Leon
Mar 28, 2025 · 5 min read
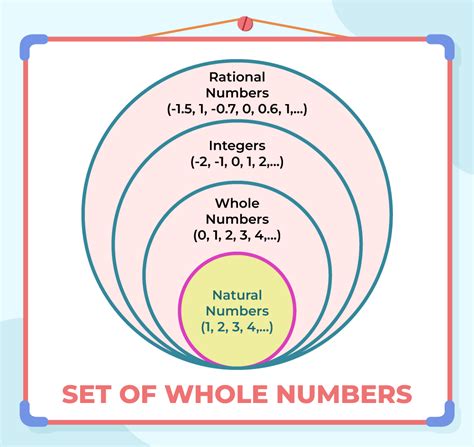
Table of Contents
Are All Whole Numbers Natural Numbers? True or False? A Deep Dive into Number Systems
The question, "Are all whole numbers natural numbers?" is a seemingly simple one, but it delves into the fundamental definitions and distinctions within the world of mathematics, specifically concerning number systems. The answer, while straightforward, requires a nuanced understanding of the properties and characteristics that define each set. Let's unpack this query completely.
Understanding Number Systems: A Foundation
Before we tackle the core question, we need a firm grasp of the different number systems involved. Mathematics uses several classifications to categorize numbers, each with unique properties:
1. Natural Numbers (Counting Numbers):
The natural numbers, often denoted by ℕ, are the numbers we use for counting. They begin with 1 and continue infinitely: {1, 2, 3, 4, 5, ...}. These are the numbers we instinctively use when counting objects. Note the crucial point: zero is not included in the natural numbers.
2. Whole Numbers:
Whole numbers, represented by ℤ₀⁺ or ℕ₀, are an extension of the natural numbers. They include all the natural numbers plus zero: {0, 1, 2, 3, 4, 5, ...}. This set is crucial for mathematical operations and representing quantities where the absence of something (zero) is a valid concept.
3. Integers:
Integers, symbolized by ℤ, encompass whole numbers and their negative counterparts: {..., -3, -2, -1, 0, 1, 2, 3, ...}. This set is fundamental for representing values that extend beyond simple counting, including concepts like debt or negative temperature.
4. Rational Numbers:
Rational numbers, denoted by ℚ, include all numbers that can be expressed as a fraction p/q, where p and q are integers and q ≠ 0. This set encompasses integers (which can be expressed as p/1), decimals that terminate (like 0.25 = 1/4), and decimals that repeat (like 0.333... = 1/3).
5. Irrational Numbers:
Irrational numbers are numbers that cannot be expressed as a fraction of two integers. These numbers have decimal representations that neither terminate nor repeat, like π (pi) ≈ 3.14159... or √2 ≈ 1.41421...
6. Real Numbers:
Real numbers, denoted by ℝ, encompass all rational and irrational numbers. This is a comprehensive set covering practically all numbers you encounter in everyday mathematics and many advanced applications.
The Crucial Difference: Zero's Inclusion or Exclusion
The key distinction between natural numbers and whole numbers hinges on the inclusion or exclusion of zero. Natural numbers start at 1, while whole numbers start at 0. This seemingly small difference has significant implications for various mathematical operations and theoretical constructs.
Answering the Question: Are All Whole Numbers Natural Numbers?
Now, armed with the definitions, we can definitively answer the question: False.
Not all whole numbers are natural numbers. While all natural numbers are whole numbers (every number in the set {1, 2, 3...} is also present in {0, 1, 2, 3...}), the converse isn't true. The whole number set contains an additional element, zero, that is absent from the natural number set. Therefore, zero is a whole number but not a natural number. This single element is enough to invalidate the statement.
Implications and Applications
The difference between natural and whole numbers may seem subtle, but it has implications across numerous mathematical fields:
- Counting: Natural numbers are ideally suited for counting discrete objects because we don't typically count "zero" objects.
- Set Theory: Understanding the distinction is fundamental in set theory, where the properties of sets are precisely defined.
- Computer Science: Programming languages often have distinct data types to represent natural numbers and whole numbers due to their different mathematical behaviors.
- Algebra and Calculus: The inclusion or exclusion of zero significantly impacts algebraic manipulations and certain calculus concepts.
- Mathematical Logic: The precise definitions help in building rigorous mathematical proofs and arguments.
Common Misconceptions and Clarifications
Several misconceptions frequently arise when discussing number systems:
- "Zero is nothing": Zero is not "nothing"; it represents the absence of quantity. It's a crucial number in mathematical operations and plays a vital role in numerous mathematical concepts.
- Interchangeability: While in many contexts, the difference might appear insignificant, the distinctions between these number systems become crucial when dealing with specialized mathematical topics.
- Confusing terms: The terminology can be confusing, particularly between whole numbers and integers. Remember that whole numbers are non-negative integers.
Expanding the Understanding: Further Exploration
The exploration of number systems doesn't end with whole and natural numbers. We've briefly touched on integers, rational numbers, irrational numbers, and real numbers. Each subsequent set expands upon the previous one, incorporating more complexity and nuance. Delving deeper into these areas reveals the rich tapestry of mathematical concepts and their interrelationships.
- Complex Numbers: Beyond real numbers lie complex numbers, which include an imaginary unit 'i', where i² = -1. These numbers are vital in various advanced mathematical fields, including engineering and physics.
- Transfinite Numbers: Stepping beyond finite numbers, we encounter transfinite numbers, which deal with infinite quantities. These are explored in set theory and have fascinating implications for understanding infinity.
Conclusion: Precision in Mathematical Definitions
The seemingly simple question of whether all whole numbers are natural numbers underscores the importance of precise mathematical definitions. The inclusion or exclusion of a single element – zero – drastically alters the nature and properties of the number set. Understanding these distinctions is fundamental for anyone pursuing mathematical studies or using mathematics in any applied field. By appreciating the nuances of different number systems, we can build a more solid and reliable understanding of the foundations of mathematics and its myriad applications. Furthermore, this understanding lays the groundwork for tackling more complex mathematical topics with greater confidence and precision. The journey into the world of numbers is an ongoing exploration, filled with intriguing concepts and profound applications.
Latest Posts
Latest Posts
-
True Or False Evaporation Is A Physical Change
Mar 31, 2025
-
Do Gram Positive Bacteria Have Porins
Mar 31, 2025
-
Which Of The Following Compounds Is Most Soluble In Water
Mar 31, 2025
-
Part Of The Brain That Controls Breathing And Heartbeat
Mar 31, 2025
-
This Pair Of Structures Anchors The Spindle
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about All Whole Numbers Are Natural Numbers True Or False . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
