A Triangle With One Right Angle Is Called A
News Leon
Mar 31, 2025 · 6 min read
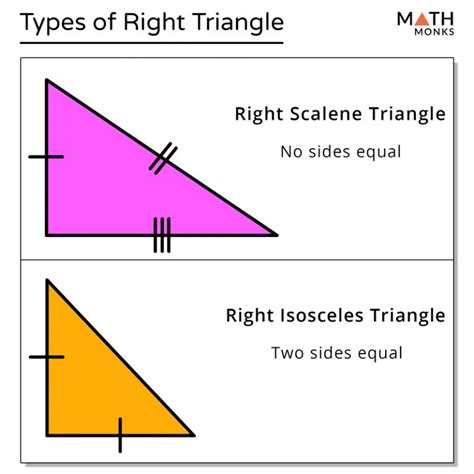
Table of Contents
A Triangle with One Right Angle is Called a Right-Angled Triangle: A Deep Dive
A triangle, the most fundamental polygon in geometry, is a closed two-dimensional figure formed by three line segments called sides and three angles formed where the sides meet. Triangles are classified based on their sides and angles, leading to several categories. One such crucial classification revolves around the measure of its angles. This article will thoroughly explore the right-angled triangle, a triangle defined by the presence of a single right angle (90 degrees). We'll delve into its properties, theorems, applications, and significance in various fields.
Understanding Right-Angled Triangles: Definition and Key Features
A right-angled triangle, also known as a right triangle, is a triangle with one of its angles measuring exactly 90 degrees. This 90-degree angle is often denoted by a small square in diagrams. The side opposite the right angle is called the hypotenuse, and the other two sides are called legs or cathetus. The legs are often referred to as the 'adjacent' and 'opposite' sides relative to a specific acute angle in the triangle.
Key characteristics of right-angled triangles include:
- One right angle (90°): This is the defining feature.
- Two acute angles: The sum of the angles in any triangle is always 180°. Since one angle is 90°, the other two angles must be acute (less than 90°) and add up to 90°.
- Hypotenuse: The hypotenuse is always the longest side of a right-angled triangle, opposite the right angle.
- Legs: The legs are the two sides that form the right angle.
The Significance of Right Angles in Geometry
Right angles hold a unique position in geometry. They represent perpendicularity, a concept crucial in many geometric constructions and calculations. The perpendicularity of the legs in a right-angled triangle forms the foundation for numerous theorems and applications, notably the Pythagorean theorem.
The Pythagorean Theorem: A Cornerstone of Right-Angled Triangle Geometry
The Pythagorean theorem is perhaps the most famous theorem associated with right-angled triangles. It establishes a fundamental relationship between the lengths of the sides:
a² + b² = c²
Where:
- a and b are the lengths of the two legs (cathetus)
- c is the length of the hypotenuse
This theorem states that the square of the hypotenuse's length is equal to the sum of the squares of the lengths of the other two sides. This theorem has far-reaching implications, allowing us to calculate the length of any side if we know the lengths of the other two.
Applications of the Pythagorean Theorem
The Pythagorean theorem is not merely a theoretical concept; it has countless practical applications in various fields:
- Construction: Determining diagonal lengths, calculating roof slopes, and laying out foundations accurately.
- Navigation: Calculating distances and bearings.
- Surveying: Measuring land areas and distances between points.
- Engineering: Designing bridges, buildings, and other structures.
- Computer graphics: Calculating distances and positions of objects in 3D space.
- Physics: Solving problems related to vectors, forces, and motion.
Trigonometric Functions and Right-Angled Triangles
Right-angled triangles are foundational to trigonometry, the branch of mathematics dealing with the relationships between angles and sides of triangles. Three primary trigonometric functions—sine (sin), cosine (cos), and tangent (tan)—are defined using the ratios of sides in a right-angled triangle:
- sin(θ) = opposite/hypotenuse
- cos(θ) = adjacent/hypotenuse
- tan(θ) = opposite/adjacent
Where θ (theta) represents one of the acute angles in the triangle. These functions allow us to determine the angles and side lengths of a right-angled triangle, provided we know at least one side and one angle (other than the right angle).
Applications of Trigonometry in Real-World Scenarios
The applications of trigonometry using right-angled triangles are extensive and span numerous fields:
- Astronomy: Calculating distances to celestial bodies.
- Navigation: Determining distances and directions.
- Physics: Analyzing projectile motion and wave phenomena.
- Engineering: Designing structures and analyzing forces.
- Mapping and surveying: Creating maps and determining locations accurately.
- Computer graphics: Creating realistic 3D models and animations.
Special Right-Angled Triangles: Isosceles and 30-60-90 Triangles
Two specific types of right-angled triangles possess unique properties:
Isosceles Right-Angled Triangles (45-45-90 Triangles)
These triangles have two legs of equal length and two angles of 45°. The ratio of their sides is always 1:1:√2 (leg:leg:hypotenuse).
30-60-90 Triangles
These triangles have angles of 30°, 60°, and 90°. The ratio of their sides is always 1:√3:2 (opposite 30°: opposite 60°: hypotenuse). These ratios simplify calculations and provide quick solutions in specific problems.
Solving Right-Angled Triangles: Methods and Techniques
Solving a right-angled triangle means finding the unknown sides and angles. This can be achieved using different techniques:
- Pythagorean theorem: To find the length of a side when the other two sides are known.
- Trigonometric functions: To find the angles or sides when one angle and one side are known.
- Special triangles: Using the ratios of sides in isosceles right-angled triangles and 30-60-90 triangles for quick calculations.
Beyond the Basics: Advanced Concepts Related to Right-Angled Triangles
The study of right-angled triangles extends beyond the basics, encompassing more advanced concepts:
- Similar triangles: Triangles with the same angles but different sizes. The ratios of corresponding sides remain constant. This concept is valuable in scaling problems and determining unknown lengths.
- Area of a right-angled triangle: Calculated using the formula: Area = (1/2) * base * height, where the base and height are the lengths of the two legs.
- Inscribed and circumscribed circles: Circles that can be inscribed within or circumscribed around a right-angled triangle, respectively. Their radii can be calculated using relationships between the sides and angles of the triangle.
- Vectors and right-angled triangles: Right-angled triangles provide a convenient way to represent vectors and resolve them into components. This has applications in physics and engineering.
Conclusion: The Enduring Importance of Right-Angled Triangles
Right-angled triangles, despite their simple definition, are fundamental to numerous areas of mathematics, science, and engineering. The Pythagorean theorem and trigonometric functions, built upon the properties of these triangles, provide powerful tools for solving problems in various fields. Understanding their properties and applications is essential for anyone pursuing studies or careers in mathematics, physics, engineering, computer science, and numerous other disciplines. Their continued relevance underscores their enduring importance in the world of mathematics and its applications. From the construction of buildings to the navigation of spacecraft, right-angled triangles play a silent but vital role in shaping our world. Their simple elegance belies their remarkable power and versatility.
Latest Posts
Latest Posts
-
What Is The Difference Between Heterochromatin And Euchromatin
Apr 02, 2025
-
In Order List The Steps Of The Scientific Method
Apr 02, 2025
-
How To Find Instantaneous Rate Of Change From A Table
Apr 02, 2025
-
Which Of The Following Will Have The Highest Boiling Point
Apr 02, 2025
-
Greatest Common Factor Of 36 And 84
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A Triangle With One Right Angle Is Called A . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
