Greatest Common Factor Of 36 And 84
News Leon
Apr 02, 2025 · 5 min read
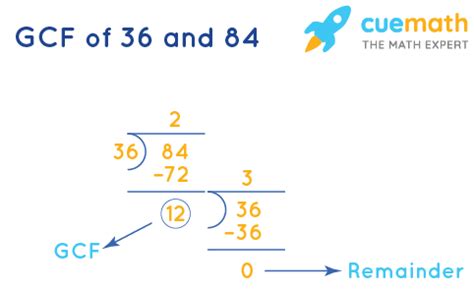
Table of Contents
Finding the Greatest Common Factor (GCF) of 36 and 84: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This article will delve deep into the methods of calculating the GCF of 36 and 84, exploring different approaches and highlighting their practical significance. We’ll move beyond simply finding the answer and explore the underlying mathematical principles, providing a comprehensive understanding for both beginners and those seeking to refresh their knowledge.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific problem of finding the GCF of 36 and 84, let's solidify our understanding of the concept. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is a straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Comparing the two lists, we see that the common factors are 1, 2, 3, 4, 6, and 12. The greatest of these is 12.
Therefore, the GCF(36, 84) = 12.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Finding all factors of very large numbers can be time-consuming.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
Prime Factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3 x 7
Now, we identify the common prime factors and their lowest powers. Both 36 and 84 have 2² and 3 as common prime factors.
GCF(36, 84) = 2² x 3 = 4 x 3 = 12
Therefore, the GCF(36, 84) = 12. This method is generally preferred for larger numbers as it's more systematic and less prone to errors.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean Algorithm to 36 and 84:
- 84 = 2 x 36 + 12 (We divide 84 by 36, getting a quotient of 2 and a remainder of 12)
- 36 = 3 x 12 + 0 (We divide 36 by the remainder 12, getting a quotient of 3 and a remainder of 0)
When the remainder becomes 0, the GCF is the last non-zero remainder. In this case, the last non-zero remainder is 12.
Therefore, the GCF(36, 84) = 12. The Euclidean Algorithm is remarkably efficient, even for very large numbers, making it a powerful tool in computational mathematics.
Applications of the Greatest Common Factor
The GCF has numerous applications across various mathematical fields and practical scenarios:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 36/84 can be simplified by dividing both the numerator and denominator by their GCF, which is 12: 36/84 = (36/12) / (84/12) = 3/7.
-
Solving Equations: The GCF plays a role in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Geometry: The GCF is used in geometric problems involving finding the dimensions of shapes with integer side lengths. For example, finding the largest square tile that can perfectly cover a rectangular floor of dimensions 36 units by 84 units.
-
Number Theory: The GCF is a fundamental concept in number theory, forming the basis for further exploration of divisibility and prime factorization.
Beyond Two Numbers: Finding the GCF of Multiple Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 36, 84, and 108, we can use the prime factorization method:
- Prime Factorization of 36: 2² x 3²
- Prime Factorization of 84: 2² x 3 x 7
- Prime Factorization of 108: 2² x 3³
The common prime factors are 2² and 3. The lowest power of 2 is 2² and the lowest power of 3 is 3¹. Therefore, the GCF(36, 84, 108) = 2² x 3 = 4 x 3 = 12.
Conclusion: Mastering the GCF
Understanding and efficiently calculating the greatest common factor is a crucial skill in mathematics. While the listing factors method is suitable for smaller numbers, the prime factorization and Euclidean Algorithm methods offer greater efficiency and applicability for larger numbers and more complex problems. The applications of the GCF extend far beyond simple arithmetic, playing a significant role in various branches of mathematics and practical problem-solving. By mastering these methods, you'll equip yourself with a powerful tool for tackling a wide range of mathematical challenges. Remember to choose the method best suited to the numbers involved for optimal efficiency and accuracy. The understanding of GCF goes beyond just finding the answer; it’s about grasping the underlying mathematical principles and recognizing its broader significance in various mathematical contexts.
Latest Posts
Latest Posts
-
Which Subshell Is Represented By The Actinides Series
Apr 03, 2025
-
Find The Area Of Scalene Triangle
Apr 03, 2025
-
Which Of The Following Is True Of Muscle Contraction
Apr 03, 2025
-
Elements That Are Liquids At Room Temperature
Apr 03, 2025
-
Direction Of Propagation Of Electromagnetic Waves
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 36 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
