A Particle Starts From The Origin At T 0
News Leon
Mar 29, 2025 · 6 min read
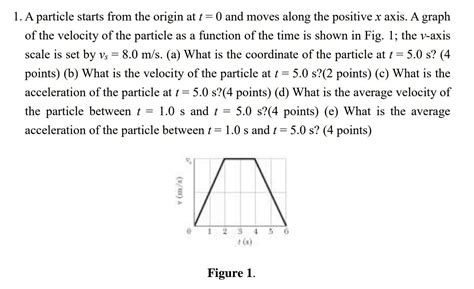
Table of Contents
A Particle Starts from the Origin at t = 0: Exploring Kinematics and Beyond
The seemingly simple statement – "a particle starts from the origin at t = 0" – forms the foundation for countless problems in physics, particularly within the realm of kinematics and dynamics. This seemingly straightforward scenario opens the door to a rich exploration of motion, involving concepts like velocity, acceleration, displacement, and their intricate relationships over time. This article delves deep into the various aspects of this fundamental problem, exploring different types of motion and the mathematical tools used to describe them.
Understanding the Fundamentals: Position, Velocity, and Acceleration
Before diving into complex scenarios, let's solidify our understanding of the basic kinematic quantities.
Position (x(t))
The position of the particle at any given time t is denoted by x(t). Since the particle starts at the origin, its initial position is x(0) = 0. The function x(t) describes the particle's location along a single dimension (we'll consider one-dimensional motion for simplicity). This function can take many forms, depending on the nature of the particle's motion.
Velocity (v(t))
Velocity represents the rate of change of position with respect to time. Mathematically, it's the first derivative of the position function:
v(t) = dx(t)/dt
Velocity is a vector quantity, possessing both magnitude (speed) and direction. A positive velocity indicates motion in the positive direction, while a negative velocity indicates motion in the negative direction. The initial velocity, v(0), can be determined from the position function by evaluating its derivative at t = 0.
Acceleration (a(t))
Acceleration describes the rate of change of velocity with respect to time. It's the first derivative of the velocity function (and the second derivative of the position function):
a(t) = dv(t)/dt = d²x(t)/dt²
Like velocity, acceleration is a vector quantity. Constant acceleration simplifies calculations considerably, but many real-world scenarios involve varying acceleration. The initial acceleration, a(0), is found by evaluating the acceleration function at t = 0.
Exploring Different Types of Motion
The type of motion the particle exhibits dictates the form of its position, velocity, and acceleration functions. Let's explore some common scenarios:
1. Uniform Motion (Constant Velocity)
In uniform motion, the particle's velocity remains constant. This implies zero acceleration: a(t) = 0. The position function becomes a simple linear equation:
x(t) = v₀t
where v₀ is the initial velocity. The graph of x(t) versus t is a straight line with a slope equal to v₀.
2. Uniformly Accelerated Motion (Constant Acceleration)
This scenario involves a constant acceleration, a. The equations of motion are:
- v(t) = v₀ + at
- x(t) = v₀t + (1/2)at²
Here, v₀ is the initial velocity. The graph of x(t) versus t is a parabola, reflecting the changing velocity. The velocity-time graph is a straight line with a slope equal to a.
3. Non-Uniform Acceleration
When the acceleration is not constant, the equations of motion become significantly more complex. We often need to resort to calculus to solve these problems. For instance, if the acceleration is a function of time, a(t), we would integrate to find the velocity and position:
- v(t) = v₀ + ∫₀ᵗ a(τ)dτ
- x(t) = ∫₀ᵗ v(τ)dτ
where τ is a dummy variable of integration. These integrals might require various integration techniques depending on the form of a(t). Numerical methods might also be necessary for complex functions.
Advanced Concepts and Applications
The basic principles of motion can be extended and applied to more complex scenarios:
Projectile Motion
Projectile motion involves the motion of an object under the influence of gravity. We typically decompose the motion into horizontal and vertical components. The horizontal motion is usually uniform (ignoring air resistance), while the vertical motion is uniformly accelerated due to gravity.
Rotational Motion
The concept of a particle starting from the origin can be extended to rotational motion, where the particle moves along a circular path. Instead of linear position, velocity, and acceleration, we use angular counterparts: angular displacement (θ), angular velocity (ω), and angular acceleration (α).
Damped Oscillations
In systems exhibiting damped oscillations (like a pendulum in a viscous medium), the particle's motion is influenced by a damping force that opposes the motion. The equations of motion become more intricate, often involving exponential decay terms.
Relativistic Motion
At speeds approaching the speed of light, the principles of Newtonian mechanics break down. Relativistic mechanics provides a more accurate description, taking into account the effects of time dilation and length contraction.
Solving Problems Involving a Particle Starting from the Origin
Let's illustrate the application of these concepts with a few examples:
Example 1: A particle starts from the origin with a constant velocity of 5 m/s. Find its position at t = 3 seconds.
This is a simple case of uniform motion. Using the equation x(t) = v₀t, we get:
x(3) = 5 m/s * 3 s = 15 m
Example 2: A particle starts from the origin with an initial velocity of 2 m/s and a constant acceleration of 3 m/s². Find its velocity and position at t = 4 seconds.
This is a case of uniformly accelerated motion. Using the equations of motion:
v(4) = 2 m/s + 3 m/s² * 4 s = 14 m/s
x(4) = 2 m/s * 4 s + (1/2) * 3 m/s² * (4 s)² = 32 m
Example 3: A particle's acceleration is given by a(t) = 2t. Find its velocity and position at t = 2 seconds, assuming it starts from rest at the origin.
This is a case of non-uniform acceleration. We need to integrate:
v(t) = ∫₀ᵗ 2τ dτ = t²
x(t) = ∫₀ᵗ τ² dτ = (1/3)t³
Therefore, at t = 2 seconds:
v(2) = 4 m/s
x(2) = (8/3) m
Conclusion
The simple premise of a particle starting from the origin at t = 0 serves as a springboard for understanding a wide range of motion types and their associated mathematical descriptions. From uniform motion to non-uniform acceleration and beyond, the concepts discussed in this article provide a robust foundation for tackling more complex problems in kinematics and dynamics. Mastering these fundamentals is crucial for progressing to more advanced topics in physics and engineering. Remember that the key to successfully solving these problems lies in clearly identifying the type of motion, selecting the appropriate equations, and carefully performing the necessary calculations. With practice, you can develop the skills necessary to confidently analyze the motion of particles and other systems.
Latest Posts
Latest Posts
-
How Many Days Are In 2016
Apr 01, 2025
-
Naoh Is Strong Or Weak Base
Apr 01, 2025
-
What Is The Decimal For 11 12
Apr 01, 2025
-
Carbon Dioxide Is Held Together By This Type Of Bond
Apr 01, 2025
-
What Is The Product Of The Reaction Shown Below
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A Particle Starts From The Origin At T 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
