Which Of The Following Quantities Is A Scalar Quantity
News Leon
Mar 28, 2025 · 6 min read
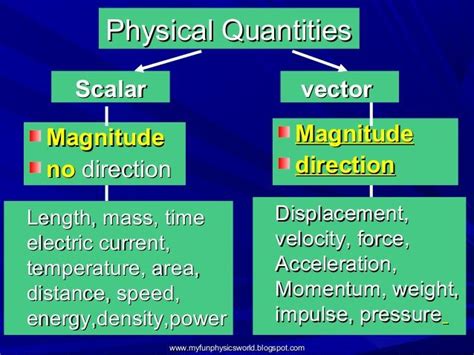
Table of Contents
Which of the Following Quantities is a Scalar Quantity? A Deep Dive into Scalars and Vectors
Understanding the difference between scalar and vector quantities is fundamental in physics and many other scientific disciplines. This article will not only define scalar and vector quantities but also delve into numerous examples, helping you confidently identify which quantities are scalar and which are vector. We'll explore the mathematical operations that apply to each, clarifying the distinctions and dispelling common misconceptions. By the end, you'll have a solid grasp of this crucial concept.
What are Scalar Quantities?
A scalar quantity is a physical quantity that is fully described by a single numerical value (magnitude) and its associated unit. It lacks a direction. Think of it simply as a number with a label. Examples include:
- Mass: Measured in kilograms (kg), grams (g), etc. A mass of 5kg simply means 5kg; there's no direction associated with it.
- Temperature: Measured in Celsius (°C), Fahrenheit (°F), Kelvin (K), etc. A temperature of 25°C is just a temperature; it doesn't point in any particular direction.
- Speed: Measured in meters per second (m/s), kilometers per hour (km/h), etc. Speed tells us how fast something is moving, not where it's going. (Note the difference between speed and velocity, discussed below.)
- Energy: Measured in Joules (J), calories (cal), etc. A system might possess 100J of energy; the energy itself isn't directional.
- Time: Measured in seconds (s), minutes (min), hours (hr), etc. Time simply progresses; it has no direction.
- Volume: Measured in cubic meters (m³), liters (L), etc. A volume of 2 liters is just a volume; it doesn't have an associated direction.
- Density: Measured in kilograms per cubic meter (kg/m³), grams per cubic centimeter (g/cm³), etc. The density of an object is a measure of its mass per unit volume, without any directional component.
- Work: Measured in Joules (J). Work done on an object is a scalar quantity even though it involves forces (vectors). The total work done is a single number.
- Power: Measured in Watts (W). Power is the rate of doing work, and like work, it is a scalar quantity.
- Electric Charge: Measured in Coulombs (C). The amount of electric charge on an object is a scalar.
Mathematical Operations with Scalars
Mathematical operations with scalars are straightforward. You can add, subtract, multiply, and divide scalar quantities without considering direction. For instance:
- 5 kg + 2 kg = 7 kg
- 10 m/s - 3 m/s = 7 m/s
- 4 J * 2 = 8 J
- 100 °C / 2 = 50 °C
What are Vector Quantities?
A vector quantity is a physical quantity that requires both magnitude and direction for its complete description. It's often represented graphically as an arrow, where the arrow's length represents the magnitude and the arrow's direction represents the direction of the quantity. Examples include:
- Displacement: The change in position of an object. A displacement of 5 meters east is different from a displacement of 5 meters west.
- Velocity: The rate of change of displacement. Velocity is a vector because it specifies both the speed and the direction of motion. A velocity of 10 m/s north is different from a velocity of 10 m/s south.
- Acceleration: The rate of change of velocity. Like velocity, acceleration is a vector quantity since it describes both how quickly the velocity is changing and in what direction.
- Force: A push or pull that can cause an object to accelerate. Force has both magnitude (strength of the push or pull) and direction.
- Momentum: The product of an object's mass and velocity. Since velocity is a vector, momentum is also a vector.
- Weight: The force of gravity on an object. Weight is a vector pointing downwards towards the center of the Earth.
- Electric Field: The electric field at a point is described by both its magnitude and direction.
- Magnetic Field: Like the electric field, the magnetic field is a vector quantity.
Mathematical Operations with Vectors
Mathematical operations with vectors are more complex than with scalars. Simple addition and subtraction require considering the direction. Vector addition typically uses the triangle rule or parallelogram rule. Multiplication involves dot products (resulting in a scalar) and cross products (resulting in a vector).
Distinguishing Between Scalars and Vectors: Common Pitfalls and Clarifications
The distinction between scalars and vectors can be subtle, and some quantities may seem ambiguous at first. Here are some clarifications:
-
Speed vs. Velocity: Speed is a scalar (magnitude only), while velocity is a vector (magnitude and direction). You can have a speed of 60 km/h, but a velocity requires specifying the direction (e.g., 60 km/h north).
-
Distance vs. Displacement: Distance is a scalar (total path length), while displacement is a vector (shortest distance between the start and end points). You could walk 100 meters in a loop, covering a distance of 100 meters, but your displacement would be 0 meters (you ended up at your starting point).
-
Work and Energy: Though work involves forces (vectors), the total work done is a scalar quantity, representing the energy transferred.
-
Magnitude of a Vector: The magnitude of a vector is always a scalar. It represents the length or size of the vector, without the direction.
Practical Applications and Real-World Examples
The difference between scalar and vector quantities is crucial in many fields:
-
Navigation: GPS systems use vector quantities (velocity, acceleration, displacement) to determine position and track movement.
-
Engineering: Structural engineers use vectors (forces, moments) to analyze stress and strain in buildings and bridges.
-
Aerospace Engineering: Aircraft flight paths and control systems rely heavily on vector calculations to manage velocity, acceleration, and trajectory.
-
Game Development: Game physics engines use vectors to simulate movement, collisions, and forces in games.
-
Medical Imaging: Vector fields are used in medical imaging techniques like magnetic resonance imaging (MRI) to represent various physical quantities within the body.
Advanced Concepts: Vector Calculus and Tensor Quantities
Beyond the basics of scalar and vector quantities, there are more advanced concepts:
-
Vector Calculus: This branch of mathematics deals with the differentiation and integration of vector fields. It's essential in various physics and engineering applications.
-
Tensor Quantities: Tensors are a generalization of scalars and vectors. A scalar is a zero-order tensor, a vector is a first-order tensor, and higher-order tensors describe more complex quantities with multiple directions and magnitudes. They are crucial in general relativity and other advanced physics areas.
Conclusion: Mastering the Scalar-Vector Distinction
Understanding the difference between scalar and vector quantities is essential for anyone working in fields that involve physics, mathematics, or engineering. By grasping the fundamental definitions, understanding the mathematical operations specific to each, and recognizing the crucial distinctions (like speed vs. velocity), you can confidently analyze and solve problems that involve these quantities. Furthermore, this knowledge provides a solid foundation for exploring more advanced concepts in mathematics and physics. Remember, scalars provide magnitude only, while vectors demand both magnitude and direction for complete description. This foundational understanding will undoubtedly enhance your ability to tackle complex scientific and engineering challenges.
Latest Posts
Latest Posts
-
When Sodium Atoms Form Sodium Ions They
Mar 31, 2025
-
Where Is The Starch Stored In Plants
Mar 31, 2025
-
When A Muscle Is Unable To Respond To Stimuli Temporarily
Mar 31, 2025
-
What Is The Empirical Formula For Glucose C6h12o6
Mar 31, 2025
-
Below Is The Structure For The Antibiotic Mycomycin
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Quantities Is A Scalar Quantity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
