What Is The Measure Of Its Complement
News Leon
Mar 30, 2025 · 5 min read
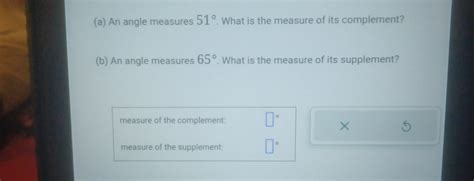
Table of Contents
What is the Measure of its Complement? A Deep Dive into Angles and Their Relationships
The question, "What is the measure of its complement?" hinges on understanding complementary angles. This seemingly simple concept underlies many geometric principles and is crucial in various fields, from architecture and engineering to computer graphics and cartography. This comprehensive guide will delve into the definition of complementary angles, explore their properties, illustrate their applications with examples, and discuss related concepts such as supplementary angles. We'll also touch on advanced applications and how to solve problems involving complementary angles.
Understanding Complementary Angles: The Fundamentals
Complementary angles are two angles whose measures add up to 90 degrees (a right angle). It's crucial to remember that the angles themselves don't need to be adjacent; they simply need to sum to 90°. This definition is the cornerstone of working with complementary angles. Think of it like this: if you have two puzzle pieces that perfectly fit together to form a right angle, those pieces represent complementary angles.
Key Characteristics of Complementary Angles:
- Sum: The defining characteristic is their sum equaling 90°.
- Individual Measures: Each angle can have any measure between 0° and 90° (exclusive), as long as their sum is 90°.
- Types of Angles: Complementary angles can be acute angles (less than 90°), but they cannot be right angles or obtuse angles (greater than 90°).
- Non-Adjacent Possibilities: Complementary angles don't have to be next to each other. They can be located anywhere in space as long as their measures add up to 90°.
Finding the Complement: Calculation Methods
Determining the measure of a complement involves straightforward arithmetic. If you know the measure of one angle, finding the measure of its complement is simply a matter of subtraction.
Method 1: Subtraction from 90°
Let's say angle A measures 30°. To find its complement (let's call it angle B), we subtract A from 90°:
90° - 30° = 60°
Therefore, the complement of a 30° angle is a 60° angle.
Method 2: Algebraic Equations
Problems often present themselves algebraically. For example:
-
Problem: Two angles are complementary. One angle is twice the measure of the other. Find the measure of each angle.
-
Solution:
-
Define Variables: Let 'x' represent the measure of the smaller angle. The larger angle would then be '2x'.
-
Set up Equation: Since the angles are complementary, their sum is 90°: x + 2x = 90°
-
Solve for x: 3x = 90° => x = 30°
-
Find the Other Angle: The larger angle is 2x = 2 * 30° = 60°
Therefore, the two complementary angles are 30° and 60°.
-
Real-World Applications of Complementary Angles
Complementary angles aren't just theoretical concepts; they appear in numerous practical applications:
1. Architecture and Construction:
-
Right Angles: Complementary angles are fundamental in ensuring structures are built with precise right angles. Builders constantly utilize the concept to guarantee the stability and integrity of buildings and other structures.
-
Roof Design: The angles of a roof's pitch and the angles formed by supporting beams often involve complementary relationships to achieve optimal strength and water runoff.
2. Engineering and Design:
-
Mechanical Systems: In designing gears, levers, and other mechanical components, complementary angles play a vital role in ensuring proper function and efficiency. The angles of force application and resulting motion are often related through complementary relationships.
-
Navigation: In navigation and surveying, complementary angles are utilized in calculations involving directions and bearings.
3. Computer Graphics and Animation:
-
Rotation and Transformation: Complementary angles are frequently used in computer graphics transformations (rotation, scaling, and shearing). Precise angle calculations are essential for creating realistic and smooth animations.
-
3D Modeling: Complementary angles are crucial in creating accurate 3D models, ensuring that surfaces and edges meet at the correct angles.
4. Cartography and Mapping:
-
Map Projections: Complementary angles are often involved in map projections, transforming the spherical surface of the earth onto a flat map. The accuracy of these projections depends on correct angle calculations.
-
Bearing and Direction: Similar to navigation, map-making utilizes complementary angles to precisely represent directions and bearings.
Beyond the Basics: Supplementary Angles and Other Relationships
While complementary angles add up to 90°, supplementary angles add up to 180°. Understanding this distinction is crucial. Many geometric problems involve both complementary and supplementary angles.
Comparing Complementary and Supplementary Angles:
| Feature | Complementary Angles | Supplementary Angles |
|---|---|---|
| Sum | 90° | 180° |
| Individual Angle Measures | Between 0° and 90° (exclusive) | Between 0° and 180° (exclusive) |
| Types of Angles | Always acute | Can be acute, right, or obtuse |
| Geometric Relationship | Angles add to a right angle | Angles add to a straight angle |
Solving Complex Problems Involving Complementary Angles
More complex problems might involve multiple complementary angle relationships, algebraic equations, and other geometric principles. Let's examine an example:
Problem: In a right-angled triangle, one acute angle is 15° more than its complement. Find the measure of each acute angle.
Solution:
-
Define Variables: Let 'x' represent the measure of one acute angle. Its complement would be 'x - 15°'.
-
Set up Equation: Since the angles are complementary, their sum is 90°: x + (x - 15°) = 90°
-
Solve for x: 2x - 15° = 90° => 2x = 105° => x = 52.5°
-
Find the Complement: The complement is x - 15° = 52.5° - 15° = 37.5°
Therefore, the two acute angles in the right-angled triangle are 52.5° and 37.5°.
Advanced Applications and Further Exploration
The concept of complementary angles extends to more advanced mathematical topics:
-
Trigonometry: The relationships between trigonometric functions (sine, cosine, tangent) are deeply connected to the relationships between complementary angles.
-
Linear Algebra: In linear algebra, complementary angles are relevant in understanding transformations of vectors and matrices.
-
Calculus: In calculus, the study of rates of change and curves often requires understanding angles and their relationships, including complementary angles.
Conclusion: Mastering the Measure of its Complement
Understanding complementary angles is essential for anyone working with geometry, whether in theoretical mathematics or practical applications. From simple calculations to complex geometric problems, the ability to determine the measure of a complement is a fundamental skill. By mastering this concept and its related principles, you unlock a deeper understanding of shapes, angles, and their role in shaping the world around us. Remember the core definition—two angles summing to 90°—and practice solving problems using both arithmetic and algebraic methods. The more you practice, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
How Many Parents Are Involved In Asexual Reproduction
Apr 01, 2025
-
What Is The Order Of The Breakdown Products Of Hemoglobin
Apr 01, 2025
-
What Muscle Subdivides The Ventral Body Cavity
Apr 01, 2025
-
How Do You Separate Iron Filings And Sand
Apr 01, 2025
-
How Many Electrons Does F Orbital Hold
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Measure Of Its Complement . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
