What Is The Area Of Triangle Qrs
News Leon
Mar 27, 2025 · 4 min read
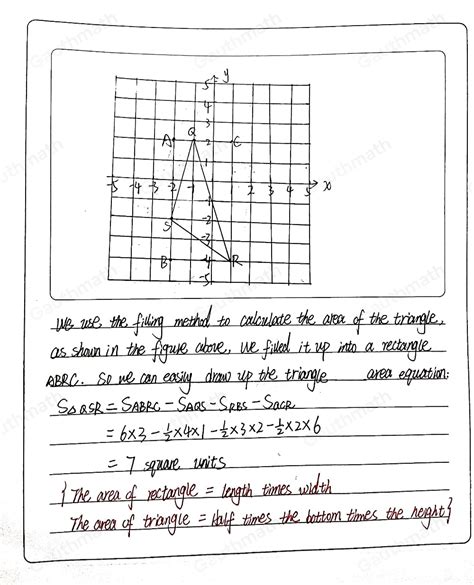
Table of Contents
What is the Area of Triangle QRS? A Comprehensive Guide
Determining the area of a triangle is a fundamental concept in geometry, applicable across various fields from architecture and engineering to computer graphics and data analysis. While the basic formula is well-known, calculating the area of a triangle, especially when dealing with coordinates or less straightforward information, requires a deeper understanding of different approaches and their applications. This comprehensive guide explores multiple methods for calculating the area of triangle QRS, covering various scenarios and providing practical examples.
Understanding the Basics: The Standard Formula
The most common method for calculating the area of any triangle is using the formula:
Area = (1/2) * base * height
This formula is intuitive and straightforward: you simply need to identify the base and the corresponding height of the triangle. The base is any one of the three sides of the triangle, and the height is the perpendicular distance from the opposite vertex to the base.
Example: If triangle QRS has a base (QR) of 10 units and a corresponding height of 6 units, then the area is:
Area = (1/2) * 10 * 6 = 30 square units
When You Know the Coordinates of the Vertices
In many real-world applications, you're given the coordinates of the vertices of the triangle, rather than the base and height directly. Let's say the coordinates of the vertices of triangle QRS are as follows:
- Q = (x₁, y₁)
- R = (x₂, y₂)
- S = (x₃, y₃)
In this case, we can use the determinant method to calculate the area. This method utilizes the concept of matrices and determinants from linear algebra. The formula is:
Area = (1/2) | x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂) |
The vertical bars indicate the absolute value, ensuring the area is always positive.
Example: Let's assume the coordinates are: Q = (1, 2), R = (4, 6), S = (7, 3). Plugging these values into the formula:
Area = (1/2) | 1(6 - 3) + 4(3 - 2) + 7(2 - 6) | = (1/2) | 3 + 4 - 28 | = (1/2) | -21 | = 10.5 square units
Heron's Formula: When You Know the Side Lengths
Heron's formula is a powerful tool when you know the lengths of all three sides of the triangle, but not the height. Let's denote the side lengths as:
- q = length of side QR
- r = length of side RS
- s = length of side SQ
First, we calculate the semi-perimeter (s):
s = (q + r + s) / 2
Then, we apply Heron's formula:
Area = √[s(s - q)(s - r)(s - s)]
Example: Let's assume the side lengths are: q = 5, r = 6, s = 7.
- Calculate the semi-perimeter: s = (5 + 6 + 7) / 2 = 9
- Apply Heron's formula: Area = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 square units
Using Trigonometry: When You Know Two Sides and the Included Angle
If you know the lengths of two sides of the triangle and the angle between them, you can utilize trigonometry to find the area. Let's say we know sides q and r, and the angle between them (∠QRS) is denoted as θ. The formula is:
Area = (1/2) * q * r * sin(θ)
Example: Let's assume q = 8, r = 10, and θ = 30 degrees.
Area = (1/2) * 8 * 10 * sin(30°) = 40 * 0.5 = 20 square units
Dealing with Special Triangles
Certain triangles have specific properties that simplify area calculations.
Equilateral Triangles:
An equilateral triangle has all three sides equal in length. If the side length is 'a', the area can be calculated using:
Area = (√3/4) * a²
Right-Angled Triangles:
A right-angled triangle has one angle equal to 90 degrees. The area is simply:
Area = (1/2) * base * perpendicular (where the base and perpendicular are the two shorter sides)
Advanced Techniques and Applications
While the methods above cover many common scenarios, more advanced techniques might be required for complex situations:
-
Integration: Calculus can be used to find the area of irregularly shaped triangles that are defined by functions rather than vertices.
-
Computer Graphics and CAD: Specialized algorithms and software are used to calculate the area of triangles within complex shapes and models. These often involve breaking down complex shapes into simpler triangular elements (triangulation).
-
Survey and Land Measurement: Precise area calculations are critical in surveying and land management, often using sophisticated surveying equipment and GPS data.
Conclusion: Choosing the Right Method
Choosing the appropriate method for calculating the area of triangle QRS depends entirely on the information you have available. If you know the base and height, the standard formula is the simplest. Coordinate information necessitates the determinant method, while Heron's formula is ideal when you only know the side lengths. Trigonometry is useful when you have two sides and the included angle. Understanding each of these methods allows you to tackle a wide range of area calculation problems with confidence and efficiency. Remember to always double-check your calculations and consider the context of your problem to ensure you're using the most appropriate and accurate method. Mastering these techniques provides a solid foundation for tackling more advanced geometrical concepts and applications.
Latest Posts
Latest Posts
-
Why Are Sex Linked Traits More Common In Males Than Females
Mar 30, 2025
-
Difference Between Specific Gravity And Density
Mar 30, 2025
-
Why Did The Pony Express Only Last 18 Months
Mar 30, 2025
-
Which Of The Following Is A True Statement About Vitamins
Mar 30, 2025
-
What Sea Separates Europe From Africa
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of Triangle Qrs . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
