What Is Cosx Sinx Equal To
News Leon
Mar 29, 2025 · 6 min read
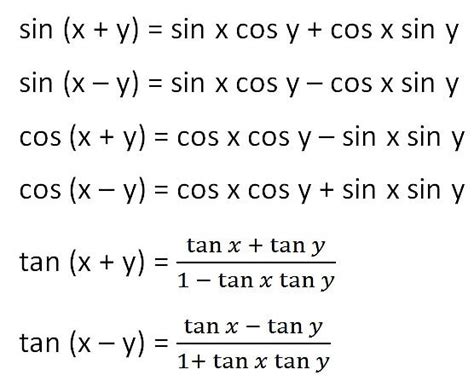
Table of Contents
What is cos(x)sin(x) equal to? A Comprehensive Exploration of Trigonometric Identities
The seemingly simple question, "What is cos(x)sin(x) equal to?" opens a door to a fascinating world of trigonometric identities and their applications in various fields, from calculus and physics to engineering and computer graphics. While there isn't a single, simplified algebraic equivalent like "x + 2", understanding how to express cos(x)sin(x) in different forms is crucial for solving complex trigonometric equations and simplifying expressions. This article delves into the various ways we can represent cos(x)sin(x), exploring its connections to other trigonometric functions and highlighting its practical significance.
Understanding the Double Angle Identities
One of the most common and useful ways to express cos(x)sin(x) involves the double angle identities. These identities relate trigonometric functions of a double angle (2x) to trigonometric functions of the single angle (x). Specifically, the crucial identity for our purpose is derived from the sine double angle formula:
sin(2x) = 2sin(x)cos(x)
By rearranging this equation, we can easily express cos(x)sin(x) as:
cos(x)sin(x) = sin(2x)/2
This is a fundamental representation, transforming a product of two trigonometric functions into a single trigonometric function of a double angle. This simplification significantly aids in solving equations and simplifying expressions. The simplicity and elegance of this transformation are key reasons why it's a frequently used identity.
Application in Calculus: Integration and Differentiation
The representation of cos(x)sin(x) as sin(2x)/2 proves invaluable in calculus. Consider the integral of cos(x)sin(x):
∫cos(x)sin(x)dx
Using the double angle identity, we can rewrite the integral as:
∫(sin(2x)/2)dx
This integral is now straightforward to solve using substitution or basic integration rules. The result is:
-cos(2x)/4 + C (where C is the constant of integration)
Similarly, the derivative of cos(x)sin(x) can be easily found using the product rule and then simplified using the double angle identities. This highlights the importance of knowing the different forms of cos(x)sin(x) for simplifying calculations in calculus.
Beyond the Double Angle: Exploring Other Representations
While the double angle identity offers a concise and frequently used representation, cos(x)sin(x) can also be expressed using other trigonometric identities. For instance, we can utilize the product-to-sum formulas. These identities transform products of trigonometric functions into sums or differences. For cos(x)sin(x), the relevant product-to-sum formula is:
cos(x)sin(x) = (1/2)[sin(x + x) - sin(x - x)]
This simplifies to:
cos(x)sin(x) = (1/2)sin(2x)
Notice that this yields the same result as derived from the double angle identity. This equivalence demonstrates the interconnectedness of various trigonometric identities, highlighting their internal consistency and providing multiple avenues for simplifying expressions.
Applications in Physics and Engineering
The ability to manipulate and simplify expressions involving cos(x)sin(x) has profound implications in physics and engineering. Many physical phenomena are modeled using sinusoidal functions, and the product of sine and cosine functions often emerges in calculations related to:
-
Wave phenomena: Interference and superposition of waves often involve expressions like cos(x)sin(x). The ability to simplify these expressions using the double angle identity makes analysis significantly easier.
-
Alternating current (AC) circuits: AC circuits involve sinusoidal currents and voltages. Calculations of power and impedance often involve products of sine and cosine functions. Understanding how to represent cos(x)sin(x) is essential for simplifying these calculations.
-
Oscillatory motion: Simple harmonic motion and other forms of oscillatory motion are often modeled using sine and cosine functions. Analysis of these systems frequently requires manipulating expressions involving products of sine and cosine, highlighting the importance of mastering these trigonometric identities.
Numerical Methods and Computational Applications
In numerical methods and computational applications, efficient representation of mathematical expressions is crucial. The simplification of cos(x)sin(x) using the double angle identity reduces computational complexity and improves efficiency. This is particularly relevant in:
-
Computer graphics: Generating realistic images and animations often involves trigonometric functions. Efficiently representing expressions such as cos(x)sin(x) directly impacts the speed and performance of rendering algorithms.
-
Signal processing: Analyzing and manipulating signals often involves Fourier transforms, which rely heavily on trigonometric functions. The ability to simplify expressions like cos(x)sin(x) contributes to more efficient signal processing algorithms.
Exploring Complex Numbers and Euler's Formula
The relationship between trigonometric functions and complex exponentials, as expressed by Euler's formula (e^(ix) = cos(x) + isin(x)), offers another perspective on cos(x)sin(x). Using Euler's formula, we can express:
sin(x) = (e^(ix) - e^(-ix))/(2i)
cos(x) = (e^(ix) + e^(-ix))/2
Multiplying these two expressions gives a complex representation of cos(x)sin(x), which can be further simplified. Although this approach leads to a more complex intermediate expression, it demonstrates the powerful connection between trigonometric functions and complex numbers, expanding the tools available for manipulating trigonometric expressions.
Practical Exercises and Problem Solving
To solidify your understanding of cos(x)sin(x) and its various representations, let's consider some practical exercises:
Exercise 1: Solve the equation cos(x)sin(x) = 1/2.
Solution: Using the double angle identity, we have sin(2x)/2 = 1/2, which simplifies to sin(2x) = 1. The general solution for 2x is 2x = π/2 + 2kπ, where k is an integer. Therefore, the general solution for x is x = π/4 + kπ.
Exercise 2: Simplify the expression 2cos(x)sin(x)cos(2x).
Solution: Using the double angle identity for sin(2x), we replace 2cos(x)sin(x) with sin(2x). The expression then becomes sin(2x)cos(2x). Further applying the double angle identity for sin(4x), which is 2sin(2x)cos(2x), we get sin(4x)/2 as the simplified expression.
These exercises illustrate how mastering the different representations of cos(x)sin(x) facilitates solving trigonometric equations and simplifying complex expressions, providing invaluable problem-solving skills.
Conclusion: Mastering Trigonometric Identities for Enhanced Problem Solving
The question of what cos(x)sin(x) is equal to doesn't have a single, simple answer. Instead, the exploration reveals a rich landscape of trigonometric identities, each offering a unique perspective and facilitating different approaches to problem-solving. From the elegant simplicity of the double angle identity to the interconnectedness revealed through the product-to-sum formulas and the broader context provided by Euler's formula, understanding these relationships is paramount for success in various fields. The ability to seamlessly translate between these different representations empowers you to tackle complex trigonometric equations, simplify complex expressions, and efficiently solve problems in calculus, physics, engineering, and computer science. Therefore, a deep understanding of cos(x)sin(x) and its multiple representations is not merely a matter of rote memorization but a crucial skill that unlocks a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
Which Organelle Is Enclosed By A Double Membrane
Mar 31, 2025
-
Compare And Contrast An Ecosystem And A Habitat
Mar 31, 2025
-
Network Layer Firewall Works As A
Mar 31, 2025
-
Is Sodium Methoxide A Strong Nucleophile
Mar 31, 2025
-
The Amount Of Space An Object Occupies
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is Cosx Sinx Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
