What Is 4 To The 5th Power
News Leon
Mar 27, 2025 · 5 min read
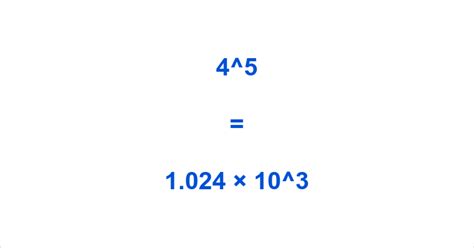
Table of Contents
What is 4 to the 5th Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics and has far-reaching applications in various fields. This comprehensive guide delves into the meaning of "4 to the 5th power," explains the concept of exponents, explores different methods for calculating it, and showcases its relevance in real-world scenarios.
Understanding Exponents
Before we tackle 4 to the 5th power, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's represented as a small number written slightly above and to the right of the base number.
For instance, in the expression 4⁵, 4 is the base and 5 is the exponent. This means we multiply 4 by itself 5 times: 4 × 4 × 4 × 4 × 4.
Key Terminology:
- Base: The number being multiplied repeatedly (in 4⁵, the base is 4).
- Exponent: The number indicating how many times the base is multiplied by itself (in 4⁵, the exponent is 5).
- Power: Another term for exponent; "4 to the 5th power" is the same as "4 raised to the power of 5."
Calculating 4 to the 5th Power
There are several ways to calculate 4⁵:
1. Manual Multiplication:
The most straightforward method is to perform the multiplication step-by-step:
4 × 4 = 16 16 × 4 = 64 64 × 4 = 256 256 × 4 = 1024
Therefore, 4 to the 5th power equals 1024.
2. Using a Calculator:
Most calculators have an exponent function (often denoted as x^y or ^). Simply enter 4, press the exponent function, enter 5, and press the equals sign (=). The calculator will directly compute the result: 1024.
3. Utilizing Properties of Exponents:
Understanding exponent properties can simplify calculations. For example:
- Product of Powers: aᵐ × aⁿ = aᵐ⁺ⁿ (When multiplying two numbers with the same base, add the exponents)
- Power of a Power: (aᵐ)ⁿ = aᵐⁿ (When raising a power to another power, multiply the exponents)
- Quotient of Powers: aᵐ / aⁿ = aᵐ⁻ⁿ (When dividing two numbers with the same base, subtract the exponents)
While these properties are not directly necessary for calculating 4⁵, they become crucial when dealing with more complex exponent expressions.
Real-World Applications of Exponents
Exponents are not just abstract mathematical concepts; they have extensive practical applications across various fields:
1. Compound Interest:
In finance, compound interest calculations rely heavily on exponents. The formula A = P(1 + r/n)^(nt) uses exponents to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t). The exponent (nt) dictates the power of compounding.
2. Population Growth:
Exponential growth models are used to predict population increases, whether it's human populations, bacterial colonies, or animal populations. The formula often involves an exponent representing the growth rate over time.
3. Radioactive Decay:
In physics, radioactive decay follows an exponential decay model. The half-life of a radioactive substance, which is the time it takes for half of the substance to decay, can be calculated using exponential functions.
4. Computer Science:
Exponents play a critical role in computer science, particularly in algorithms and data structures. Binary numbers, the foundation of computer operations, are based on powers of 2. Big O notation, used to describe the efficiency of algorithms, often involves exponential functions to represent the growth rate of computation time with respect to input size.
5. Geometry:
In geometry, exponents are used in calculating areas and volumes of shapes. For example, the area of a square is side², and the volume of a cube is side³.
6. Physics and Engineering:
Exponents appear extensively in physics and engineering equations, including those describing motion, energy, and wave phenomena.
Expanding on the Concept: Higher Powers and Negative Exponents
While we've focused on 4⁵, it's important to understand how the concept extends to higher powers and negative exponents.
Higher Powers:
Calculating 4⁶, 4⁷, or even higher powers simply involves continuing the multiplication process. The larger the exponent, the faster the result grows. This rapid growth is characteristic of exponential functions.
Negative Exponents:
A negative exponent indicates the reciprocal of the positive power. For instance, 4⁻⁵ is the reciprocal of 4⁵:
4⁻⁵ = 1 / 4⁵ = 1 / 1024
This means that a negative exponent results in a fractional value, less than 1.
Fractional Exponents:
Fractional exponents represent roots. For example, 4^(1/2) is the square root of 4 (which is 2), and 4^(1/3) is the cube root of 4. More generally, a^(m/n) is the nth root of a raised to the power of m.
Conclusion: The Significance of 4 to the 5th Power and Exponents in General
Understanding "4 to the 5th power" is not merely about calculating 1024; it's about grasping the fundamental concept of exponents and their widespread applications. From financial calculations to scientific modeling and computer algorithms, exponents form a cornerstone of numerous fields. By mastering this concept, you open doors to deeper comprehension in mathematics and its practical relevance in the real world. Remember, the seemingly simple act of raising a number to a power unlocks powerful tools for understanding and solving complex problems.
Latest Posts
Latest Posts
-
Is Iodine A Metal Or Nonmetal
Mar 30, 2025
-
Find The Area Of The Parallelogram Shown
Mar 30, 2025
-
All Except Which Of The Following Are Homologous Structures
Mar 30, 2025
-
Which Of The Following Is Not True About Natural Selection
Mar 30, 2025
-
What Part Of A Carrot Do We Eat
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 5th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
