Triangle With 3 Lines Of Symmetry
News Leon
Mar 26, 2025 · 6 min read
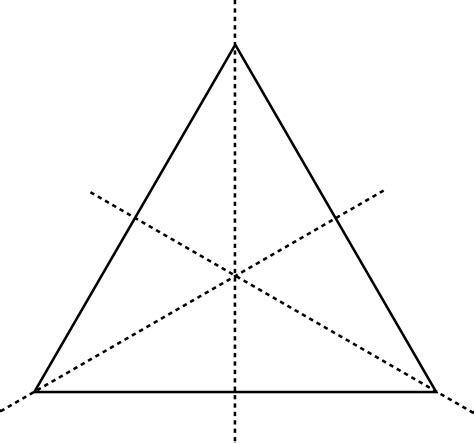
Table of Contents
Triangle with 3 Lines of Symmetry: Exploring the Equilateral Triangle
The world of geometry is rich with fascinating shapes, each possessing unique properties and characteristics. Among these, the triangle stands out as a fundamental building block, its versatility evident in countless applications from architecture to art. But not all triangles are created equal. While many triangles boast a single or perhaps two lines of symmetry, a special class exists that possesses a remarkable three: the equilateral triangle. This article delves deep into the properties of this exceptional shape, exploring its symmetries, geometric relationships, and its significance across various fields.
Understanding Lines of Symmetry
Before diving into the specifics of equilateral triangles, let's establish a firm understanding of what a line of symmetry actually is. A line of symmetry, also known as a line of reflection or axis of symmetry, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, the two halves would perfectly overlap.
Many shapes possess lines of symmetry. A square, for instance, has four lines of symmetry: two that run diagonally and two that run horizontally and vertically. A circle, interestingly, has infinite lines of symmetry, as any line passing through its center will divide it into two identical halves. Triangles, however, exhibit a more nuanced range of symmetry.
The Uniqueness of the Equilateral Triangle
The equilateral triangle stands apart from other types of triangles due to its exceptional symmetry. An equilateral triangle is a triangle in which all three sides are of equal length. This inherent equality of sides directly leads to its three lines of symmetry.
Three Lines of Symmetry: A Detailed Look
Each line of symmetry in an equilateral triangle connects a vertex (corner) to the midpoint of the opposite side. These lines are also known as medians, altitudes, angle bisectors, and perpendicular bisectors. This remarkable confluence of properties is unique to the equilateral triangle. Let's break down each role:
-
Median: A median connects a vertex to the midpoint of the opposite side. In an equilateral triangle, the median bisects the opposite side, creating two equal segments.
-
Altitude: An altitude is a perpendicular line segment from a vertex to the opposite side. In an equilateral triangle, the altitude is perpendicular to the base and bisects it.
-
Angle Bisector: An angle bisector divides an angle into two equal angles. In an equilateral triangle, the line of symmetry bisects the angle at the vertex, creating two 30-degree angles.
-
Perpendicular Bisector: A perpendicular bisector is a line that intersects a line segment at a right angle at its midpoint. The lines of symmetry in an equilateral triangle are perpendicular bisectors of the opposite sides.
This convergence of properties highlights the inherent balance and regularity of the equilateral triangle. No other triangle type displays this perfect symmetry.
Geometric Properties and Relationships
The equilateral triangle's three lines of symmetry are not merely aesthetic features; they are fundamental to its geometric properties. These properties enable various calculations and constructions:
-
Angles: All three interior angles of an equilateral triangle measure 60 degrees. This is a direct consequence of its symmetry – the three lines of symmetry divide the triangle into six congruent 30-60-90 triangles.
-
Area Calculation: The area of an equilateral triangle can be easily calculated using its side length (a). The formula is: Area = (√3/4) * a². This formula is directly derived from its symmetrical properties.
-
Circumcenter and Incenter: The circumcenter (the center of the circle passing through all three vertices) and the incenter (the center of the inscribed circle) coincide in an equilateral triangle. This point is also the centroid (the intersection of the medians) and orthocenter (the intersection of the altitudes). This unique coincidence is a direct result of its high degree of symmetry.
-
Regular Polygon Connection: The equilateral triangle is the simplest example of a regular polygon – a polygon with all sides and angles equal. Understanding its properties provides a solid foundation for exploring other regular polygons such as squares, pentagons, and hexagons.
Applications in Various Fields
The equilateral triangle's unique properties and striking symmetry have found applications across various fields:
-
Architecture and Design: Equilateral triangles appear frequently in architectural designs, often forming the basis of stable and aesthetically pleasing structures. Think of the triangular supports used in bridges or the triangular patterns found in various building facades. The inherent strength of the equilateral triangle makes it an ideal structural element.
-
Art and Design: Equilateral triangles are used extensively in art and design for their visual appeal and symbolic significance. They appear in logos, patterns, and decorative motifs, often representing balance, stability, and harmony. Its symmetrical nature lends itself well to creating visually pleasing compositions.
-
Mathematics and Geometry: As a fundamental geometric shape, the equilateral triangle plays a crucial role in various mathematical concepts and proofs. It is frequently used to illustrate geometric theorems, especially those involving symmetry, congruence, and similarity.
-
Physics and Engineering: The equilateral triangle's symmetrical nature is utilized in engineering for applications requiring balanced forces or even distribution of weight.
-
Nature: Surprisingly, equilateral triangles are found naturally in crystal structures and certain molecular arrangements. While not perfectly equilateral, these natural occurrences demonstrate the importance of this shape in the natural world.
Beyond the Basics: Exploring Tessellations and Fractals
The equilateral triangle's symmetry also leads to fascinating explorations in tessellations and fractals.
-
Tessellations: Equilateral triangles can perfectly tessellate – meaning they can be arranged to cover a plane without any gaps or overlaps. This property is exploited in creating various patterns and tilings. The hexagonal tiling found in honeycombs is a prime example, indirectly related to equilateral triangles.
-
Fractals: Equilateral triangles are used as the base for constructing various fractals, generating complex patterns with self-similar structures. The Sierpinski triangle, a classic fractal, is built by repeatedly subdividing an equilateral triangle.
Conclusion: The Enduring Significance of the Equilateral Triangle
The equilateral triangle, with its three lines of symmetry, stands as a testament to the elegance and power of mathematical harmony. Its unique properties extend beyond mere geometric definitions, impacting various fields from architecture and art to mathematics and science. The simplicity of its structure belies its profound impact, making it a shape of enduring significance across disciplines. From its simple construction to its complex implications in tessellations and fractals, the equilateral triangle continues to fascinate and inspire. Its inherent symmetry provides a perfect example of balance and order in the world of geometry and beyond. Further exploration of its properties and applications promises continued discoveries and insights into the beauty of this remarkable shape.
Latest Posts
Latest Posts
-
Earth Is Approximately A Sphere Of Radius 6 37
Mar 29, 2025
-
Is Salt Water A Heterogeneous Mixture
Mar 29, 2025
-
What Is The Opposite Word Of Innocent
Mar 29, 2025
-
How Much Days Is 48 Hours
Mar 29, 2025
-
Select The Correct Iupac Name For The Compound Shown
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Triangle With 3 Lines Of Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
