The Simplest Rationalising Factor Of Root 50
News Leon
Mar 29, 2025 · 4 min read
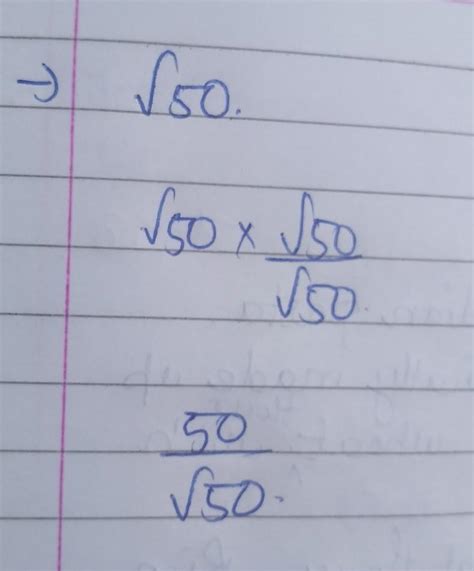
Table of Contents
The Simplest Rationalising Factor of √50: A Deep Dive into Surds
Rationalizing the denominator, a cornerstone of simplifying algebraic expressions, often involves dealing with surds – numbers that are the square root of non-perfect squares. This article will focus on finding the simplest rationalizing factor for √50, exploring the underlying concepts and demonstrating various methods to achieve this. We’ll delve into the fundamental principles of surds, explaining why rationalizing is crucial, and exploring how to approach this specific problem efficiently and effectively. We’ll also look at related problems to solidify understanding.
Understanding Surds and Rationalization
A surd is an irrational number that can be expressed as the root of an integer. √50 is a surd because 50 is not a perfect square. A rational number can be expressed as a fraction p/q, where p and q are integers, and q ≠ 0. Rationalizing the denominator involves manipulating an expression containing a surd in the denominator to produce an equivalent expression with only rational numbers in the denominator. This process improves the readability and simplifies further calculations.
Why Rationalize?
There are several compelling reasons to rationalize denominators:
- Simplicity and Readability: Expressions with rational denominators are generally easier to understand and work with.
- Standardization: Rationalizing the denominator is a common practice in mathematics, promoting consistency and making it easier for others to understand your work.
- Accuracy in Calculations: Decimal approximations of surds can lead to rounding errors. Working with rationalized forms reduces this potential for error.
- Further Simplification: In more complex calculations, having a rational denominator often simplifies subsequent steps.
Finding the Simplest Rationalizing Factor of √50
The key to rationalizing √50 lies in simplifying the surd first. We need to find the prime factorization of 50:
50 = 2 x 5 x 5 = 2 x 5²
Therefore, √50 can be simplified to:
√50 = √(2 x 5²) = √2 x √5² = 5√2
Now, we need to find a factor that, when multiplied by 5√2, results in a rational denominator. This is achieved by multiplying by √2.
The simplest rationalizing factor for √50 is therefore √2.
Let’s see this in action:
1/√50 = 1/(5√2)
Multiplying both the numerator and denominator by √2:
(1 x √2) / (5√2 x √2) = √2 / (5 x 2) = √2 / 10
The denominator is now rational, and the expression is simplified.
Alternative Approaches and Considerations
While multiplying by √2 is the most direct approach, let's explore other perspectives to enhance understanding:
1. Direct Rationalization of √50:
Instead of simplifying √50 first, we could directly rationalize 1/√50 by multiplying the numerator and the denominator by √50:
(1 x √50) / (√50 x √50) = √50 / 50 = (5√2) / 50 = √2 / 10
This method achieves the same result, although it involves slightly more simplification steps.
2. Generalizing the Concept:
The simplest rationalizing factor for a surd of the form √a (where 'a' is a non-perfect square) is always √a itself. This is because multiplying √a by √a always results in 'a', a rational number.
3. Dealing with More Complex Expressions:
Consider the expression 1/(√50 + √2). Here, we use the conjugate to rationalize. The conjugate of √50 + √2 is √50 - √2.
Multiplying both the numerator and denominator by the conjugate:
[1(√50 - √2)] / [(√50 + √2)(√50 - √2)]
Applying the difference of squares (a+b)(a-b) = a² - b² in the denominator:
(√50 - √2) / (50 - 2) = (√50 - √2) / 48 = (5√2 - √2) / 48 = 4√2 / 48 = √2 / 12
In this case, the rationalizing factor is the conjugate, not simply √2.
Practicing with Similar Surds
To further solidify our understanding, let’s apply the principles to similar surds:
1. Rationalizing √72:
√72 = √(2 x 36) = √(2 x 6²) = 6√2
The simplest rationalizing factor is √2.
2. Rationalizing √125:
√125 = √(5 x 25) = √(5 x 5²) = 5√5
The simplest rationalizing factor is √5.
3. Rationalizing √18:
√18 = √(2 x 9) = √(2 x 3²) = 3√2
The simplest rationalizing factor is √2.
Conclusion: Mastering Rationalization
Rationalizing the denominator is a fundamental skill in algebra. Finding the simplest rationalizing factor for √50 and similar surds requires understanding prime factorization and the properties of surds. We've seen that the simplest rationalizing factor for √50 is √2, leading to a simplified, rationalized expression of √2/10. This process, while seemingly simple, is critical for effective algebraic manipulation and accurate calculations involving irrational numbers. By practicing with various surds and applying the methods discussed, you will build a strong foundation in simplifying algebraic expressions and enhance your mathematical problem-solving abilities. Remember to always simplify the surd before identifying the rationalizing factor for the most efficient solution. This detailed exploration provides a comprehensive understanding of the process and its application in diverse scenarios.
Latest Posts
Latest Posts
-
In A Chemical Reaction Matter Is Neither Created Nor Destroyed
Mar 31, 2025
-
Which Of These Is Not An Endocrine Gland
Mar 31, 2025
-
Evolution Can Best Be Defined As
Mar 31, 2025
-
Is Sulfur More Electronegative Than Oxygen
Mar 31, 2025
-
What Is The Molar Mass Of Al No3 3
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about The Simplest Rationalising Factor Of Root 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
